前排提示:本文的前两节仅限学有余力的同学研究
在文章 论极值点偏移 中，我介绍了极值点偏移问题最常用的两种方法：构造函数法和比值/差值换元法。本文将介绍两种进阶方法：放缩和拟合，此外，还将介绍一种题型：拐点偏移。
1. 放缩
放缩法要求你熟记各种常用的导数不等式，移步另一篇文章：常用导数不等式汇总 。
在选择用什么不等式进行放缩的时候，需要保证选择的不等式的取等条件与待证不等式的取等条件一致。
下面举几个例子
问题
已知函数 $f(x) = \frac{(x-1)\ln{x}}{x}$，$f(x_1) = f(x_2)$，$x_1\neq x_2$，证明：$x_1x_2 > 1$ 。
解析：
本题用构造函数法或比值换元法也可以轻松解决。下面使用放缩法，首先讨论 $x_1,x_2$ 的范围。对 $f(x)$ 求导 $f'(x) = \frac{\ln{x}+x-1}{x^2}$ ，分母是单增的，零点为 $1$ ，故 $f(x)$ 先减后增，极小值点为 $1$ 。不妨设 $x_1 < x_2$，则 $x_1 < 1 < x_2$ 。
由条件 $f(x_1) = f(x_2)$ 得
应用不等式 $\ln{x} \leq x-1$ ，得
$$ \frac{(x_1-1)^2}{x_1} < \frac{(x_1-1)\ln{x_1}}{x_1} = \frac{(x_2-1)\ln{x_2}}{x_2} < \frac{(x_2-1)^2}{x_2} $$注意上面两个不等号反向的原因是 $x_1-1$ 是负的， $x_2-1$ 是正的。于是我们有
$$ \frac{(x_1-1)^2}{x_1} < \frac{(x_2-1)^2}{x_2} $$化简后，即得 $x_1x_2 > 1$ 。如果是考试，上面使用 $\ln{x} \leq x-1$ 之前需要先证明。这里选择这个不等式进行放缩，是考虑到其取等条件为 $x=1$ ，而本题的待证不等式的“取等条件”也是 $x_1=x_2=1$ 。如果你选择不等式 $\ln{x} \leq \frac{x}{e}$ 进行放缩，则不能证得结果，因为这个不等式的取等条件是 $x = e$ 。
问题
已知函数 $f(x) = x - \ln{x}$，$f(x_1) = f(x_2) = a$，$x_1\neq x_2$，证明：$x_1 + x_2 > 1+a$。
首先讨论 $x_1,x_2$ 的范围。求导 $f'(x) = 1 - \frac{1}{x}$ ，$f(x)$ 先减后增，极小值点为 $1$ 。不妨设 $x_1 < x_2$ ，则 $0 < x_1 < 1 < x_2$ 。
由条件 $f(x_1) = f(x_2) = a$ ，得
本题待证不等式的取等条件不明，但根据函数的极值点为 1 ，我们倾向于选择取等条件为 1 的不等式进行放缩。应用下面的不等式：
$$ \begin{cases} \ln{x} < \frac{2(x-1)}{x+1} & 0 < x < 1\\ \ln{x} > \frac{2(x-1)}{x+1} & x > 1 \end{cases} $$得到
$$ x_1 - \frac{2(x_1-1)}{x_1+1} < x_1-\ln{x_1} = x_2 - \ln{x_2} = a < x_2 - \frac{2(x_2-1)}{x_2+1} $$即
$$ \left\{ \begin{align*} x_1 - \frac{2(x_1-1)}{x_1+1} &< a \\ x_2 - \frac{2(x_2-1)}{x_2+1} &> a \end{align*} \right. $$即
$$ \left\{ \begin{align*} x_1^2 - (a+1)x_1 + 2-a &< 0\\ x_2^2 - (a+1)x_2 + 2-a &> 0 \end{align*} \right. $$即
$$ x_1^2 - (a+1)x_1 + 2 - a < x_2^2 -(a+1)x_2+2-a $$整理即得 $x_1 + x_2 > 1 + a$ 。
选择放缩不等式是一个不断试错的过程。本题如果选择其它取等条件为 $1$ 的不等式进行放缩，则会得到不一样的结果。例如，选择不等式
则会得到 $x_1 + x_2 < 2a$ 。如果选择不等式
$$ \begin{cases} \ln{x} > \sqrt{x} - \frac{1}{\sqrt{x}} & 0 < x < 1\\ \ln{x} < \sqrt{x} - \frac{1}{\sqrt{x}} & x > 1 \end{cases} $$则会得到 $\sqrt{x_1} + \sqrt{x_2} < a$ 。这两种结果的不等号都与本题待证不等式的不等号相反，这是因为这两种放缩不等式的不等号都与本题使用的放缩不等式相反！
2. 拟合
拟合法要求你知道泰勒公式。限于篇幅，本文并不打算介绍泰勒公式，你可以自行查阅其它资料，或者参考本博客的其它文章（如果写了的话），标签为
(如果点进去是404页面，那就还没写)拟合法其实跟上面讲的放缩法差不多，唯一的区别是，拟合法中用来放缩的不等式是我们通过二阶泰勒公式得到的。下面是一些例子：
问题
已知函数 $f(x) = x\ln{x}$，$f(x_1) = f(x_2)$，$x_1 \neq x_2$，证明：$x_1 + x_2 > \frac{2}{e}$。
解析：
首先，讨论 $x_1,x_2$ 的范围。$x\ln{x}$ 是常见函数，图像要熟记：
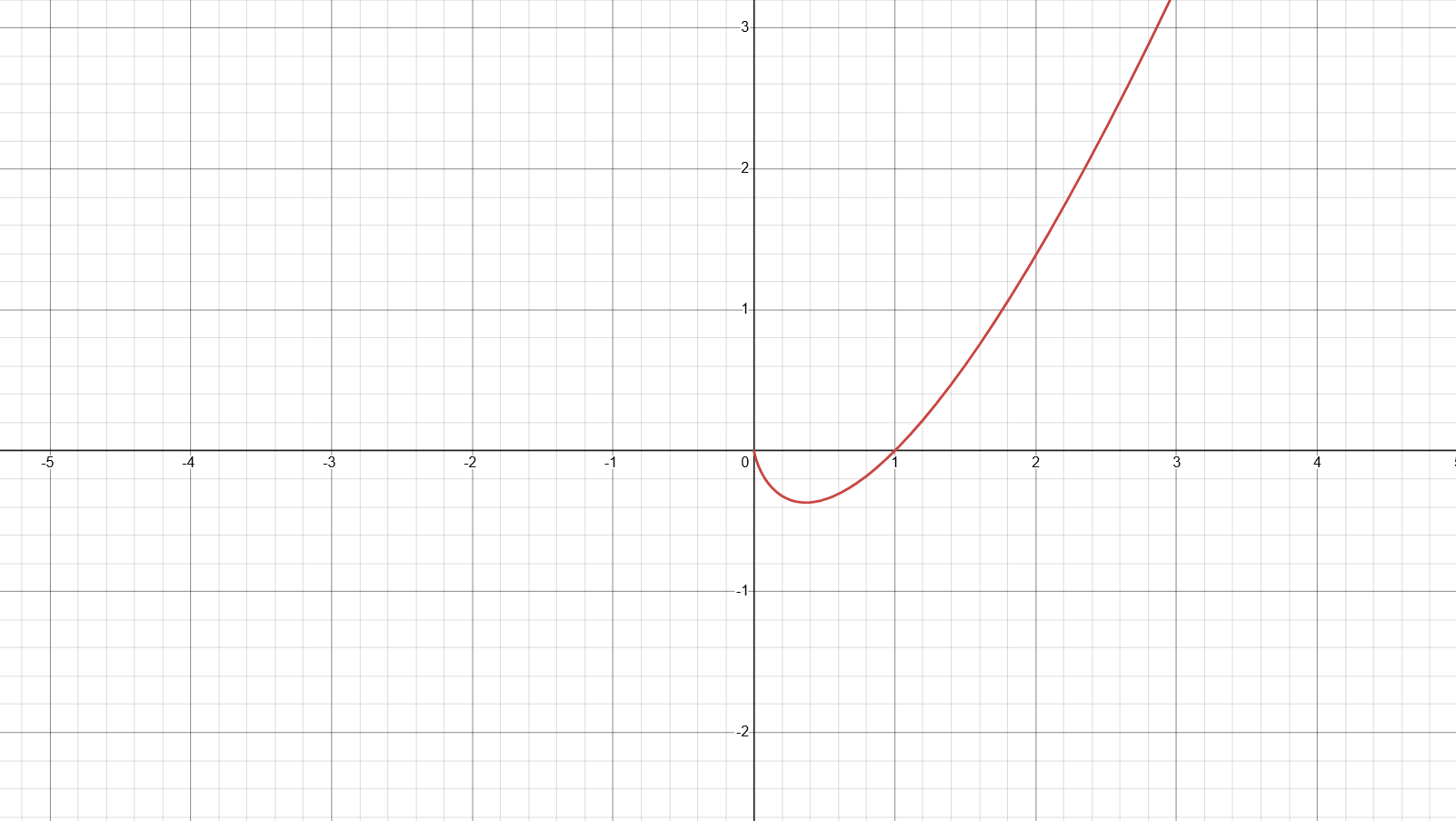
务必记住当 $x\to0$ 时，$x\ln{x}\to 0$ 。不妨设 $x_1 < x_2$，则 $0 < x_1 < \frac{1}{e} < x_2 < 1$ 。由于待证不等式的取等条件是 $x_1 = x_2 = \frac{1}{e}$ ，于是我们在 $x = \frac{1}{e}$ 处进行二阶泰勒展开：
$$ g(x) = f(\frac{1}{e}) + f'(\frac{1}{e})(x-\frac{1}{e})+\frac{f''(\frac{1}{e})}{2}(x-\frac{1}{e})^2 $$计算得 $g(x) = -\frac{1}{e} + \frac{e}{2}(x-\frac{1}{e})^2$ 。我们希望有下面的不等式成立：
$$ \left\{ \begin{align*} f(x) &> g(x) && 0 < x < \frac{1}{e}\\ f(x) &< g(x) && \frac{1}{e} < x < 1 \end{align*} \right. $$接下来我们验证 $f(x)$ 与 $g(x)$ 之间是否存在上述不等式。构造函数
$$ h(x) = f(x) - g(x) = x\ln{x} +\frac{1}{e} - \frac{e}{2}(x-\frac{1}{e})^2 $$求导
$$ h'(x) = \ln{x} - ex + 2 $$单调性不明显，继续求导 $h''(x) = \frac{1}{x} - e$ ，于是 $h'(x)$ 的最大值为 $h(\frac{1}{e}) = 0$ ，则 $h'(x) \leq 0$ ，$h(x)$ 单调递减。又因为 $h(\frac{1}{e}) = 0$，故当 $0 < x < \frac{1}{e}$ 时，$h(x) > 0$；当 $x > \frac{1}{e}$ 时，$h(x) < 0$ 。即
$$ \begin{cases} f(x) > -\frac{1}{e} + \frac{e}{2}(x-\frac{1}{e})^2 & 0 < x < \frac{1}{e}\\ f(x) < -\frac{1}{e} + \frac{e}{2}(x-\frac{1}{e})^2 & x > \frac{1}{e} \end{cases} $$这就是我们要用来放缩的不等式了。应用在 $f(x_1) = f(x_2)$ 上，就有
$$ -\frac{1}{e} + \frac{e}{2}(x_1-\frac{1}{e})^2 < f(x_1) = f(x_2) < -\frac{1}{e} + \frac{e}{2}(x_2-\frac{1}{e})^2 $$整理即得 $x_1 + x_2 > \frac{2}{e}$ 。
在考试的时候，你不需要写出泰勒公式，或者说不需要写出函数 $g(x)$ 的构造过程，直接从 $h(x)$ 开始写起即可，这在逻辑上完全没有问题，只是如果阅卷老师不了解这种方法的话，会觉得难以理解。下面这道题，我就用这种方式写解析：
问题
已知函数 $f(x) = x - \ln{x}$，$f(x_1) = f(x_2)$，$x_1\neq x_2$，证明：$x_1 + x_2 > 2$。
解析：
求导 $f'(x) = 1 - \frac{1}{x}$，当 $0 < x < 1$ 时，$f'(x) < 0$，$f(x)$ 单减；当 $x > 1$ 时，$f'(x) > 0$，$f(x)$ 单增。不妨设 $x_1 < x_2$，则 $x_1 < 1 < x_2$ 。构造函数
求导 $g'(x) = -\frac{(x-1)^2}{x} < 0$ ，$g(x)$ 单减。又因为 $g(1) = 0$，故
$$ \begin{cases} x - \ln{x} > 1 + \frac{1}{2}(x-1)^2 & 0 < x < 1\\ x - \ln{x} < 1 + \frac{1}{2}(x-1)^2 & x > 1 \end{cases} $$由于 $f(x_1) = f(x_2)$ ，根据上面的不等式，有
$$ 1 + \frac{1}{2}(x_1-1)^2 < f(x_1) = f(x_2) < 1 + \frac{1}{2}(x_2-1)^2 $$整理即得 $x_1 + x_2 > 2$ 。
上面的解答，完全隐藏了函数 $g(x)$ 的构造过程。不了解拟合法的人看到这个过程，会觉得惊为天人、神之一手。
下面这道题，不能使用拟合法。
问题
已知函数 $f(x) = \frac{e^x}{x}$，$f(x_1) = f(x_2)$，$x_1\neq x_2$，证明：$x_1 + x_2 > 2$。
解析：
首先，讨论 $x_1,x_2$ 的范围，求导 $f'(x) = \frac{(x-1)e^x}{x^2}$，$f(x)$ 先减后增，极小值点为 $1$ 。图像大致如下：
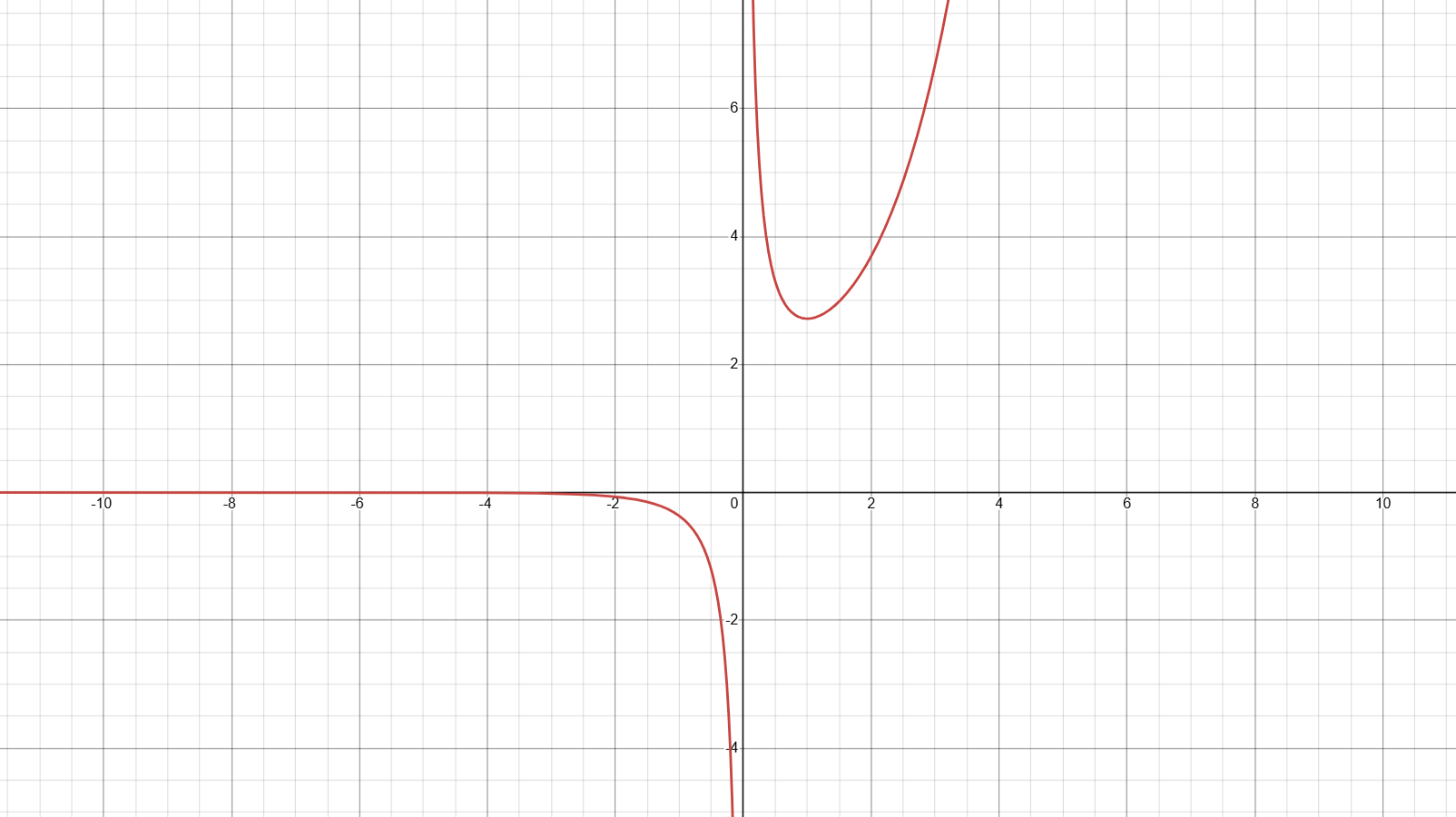
不妨设 $x_1 < x_2$，则 $0 < x_1 < 1 < x_2$ 。考虑到待证不等式的取等条件是 $x_1 = x_2 = 1$ ，因此我们对 $f(x)$ 在 $x=1$ 处进行二阶泰勒展开，得到
$$ \begin{align*} g(x) &= f(1) + f'(1)(x-1) + \frac{f''(1)}{2}(x-1)^2\\ &= e + \frac{e}{2}(x-1)^2 \end{align*} $$我们希望有下面的不等式成立：
$$ \left\{ \begin{align*} f(x) &< g(x) && 0 < x < 1\\ f(x) &> g(x) && x > 1 \end{align*} \right. $$下面我们验证 $f(x)$ 与 $g(x)$ 之间的不等关系。构造函数 $h(x) = f(x) - g(x)$ ，求导
$$ h'(x) = \frac{(x-1)(e^x-ex^2)}{x^2} $$很明显，我们还要研究 $e^x - ex^2$ 的性质。令 $j(x) = e^x - ex^2$，求导得 $j'(x) = e^x - 2ex$，性质仍不明确，继续求导得 $j''(x) = e^x - 2e$，则 $j'(x)$ 先减后增，最小值 $j'(\ln{2e}) = 2e(1-\ln{2e}) < 0$，又因为在两侧无穷处，$j'(x)\to+\infty$，故 $j'(x)$ 图像大致如下：
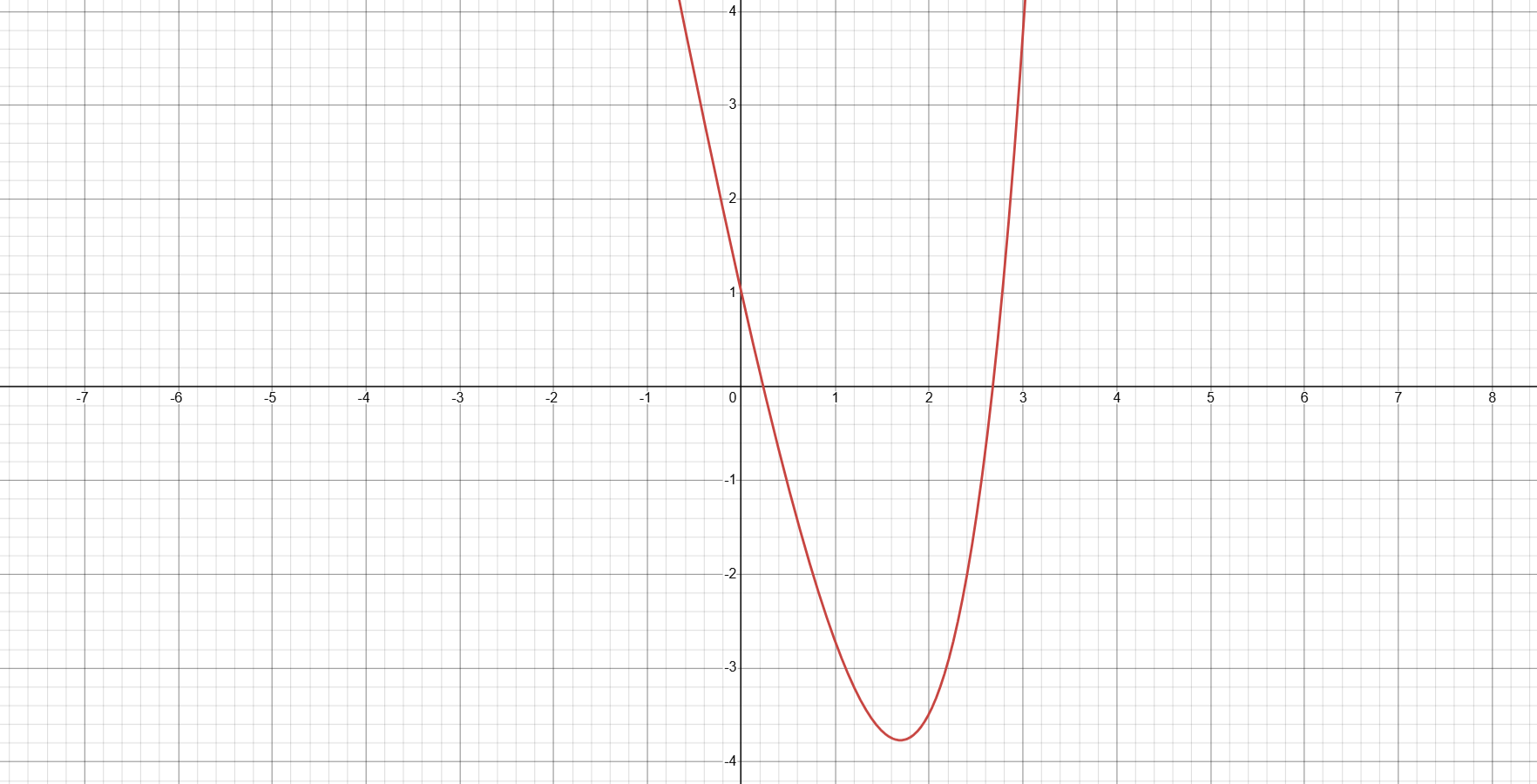
注意 $j'(0) = 1 > 0$ 。由于 $0 < x_1 < 1 < x_2$，我们实际上只需要考虑 $x > 0$ 的区域。由上图可知，$j(x)$ 先增后减再增，再根据几个关键点：$j(0) = 1,j(1) = 0,j(+\infty) = +\infty$，可以画出其大致图像如下：
于是，当 $0 < x < 1$ 时，$h'(x) < 0$；当 $x > 1$ 时，我们希望能有 $h'(x) > 0$ 恒成立，但由上图知 $j(x)$ 在 $x > 1$ 的区域一开始是小于 $0$ 的，此时 $h'(x) < 0$ ，这就不能得到我们想要的不等式了。因此，本题是不能用拟合法做的，可以用构造函数法或者差值换元法解决。
3. 拐点偏移
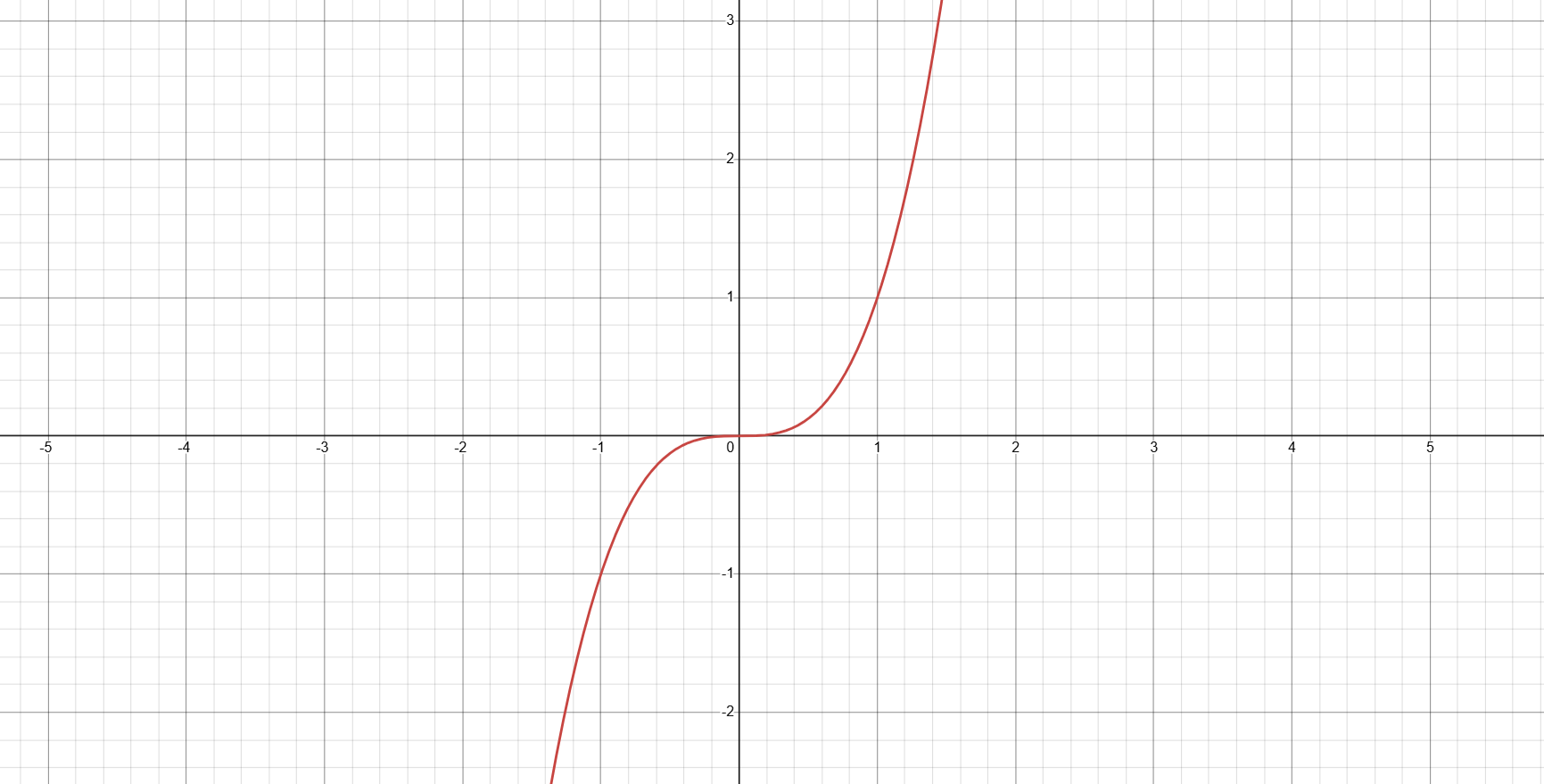
极值点是 $f'(x)$ 的变号零点，而拐点是 $f''(x)$ 的变号零点。从几何上看，极值点是函数单调性改变的分界点，而拐点则是函数凹凸性改变的分界点。典型的例子是 $f(x) = x^3$ ，其二阶导 $f''(x) = 6x$，拐点为 $x= 0$ 。从图像上看，在拐点左侧，函数上凸；在拐点右侧，函数下凸。
拐点偏移与极值点偏移的区别在于，条件 $f(x_1) = f(x_2)$ 换成了 $f(x_1) + f(x_2) = C$，其中 $C$ 是一个常数，常规情况下，$C$ 是拐点处函数值的两倍，即 $C = 2f''(x_0)$，其中 $x_0$ 是拐点。至于做法，和极值点偏移差不多，一般使用构造函数法。举个例子：如果条件为 $f(x_1) + f(x_2) = 1$，待证不等式为 $x_1 + x_2 > 2$，则把待证不等式转化为比较 $f(x_1)$ 与 $f(2-x_2)$ 的大小，再转化为比较 $1-f(x_2)$ 和 $f(2-x_2)$ 的大小，构造函数 $g(x) = 1 - f(x) - f(2-x)$ 即可。
下面是一个拐点偏移的例子：
问题
已知函数 $f(x) = 2\ln{x} + x^2 - 1$，$f(x_1) + f(x_2) = 0$，$x_1\neq x_2$，证明：$x_1 + x_2 > 2$
解析：
首先讨论 $x_1,x_2$ 的范围。由于 $f(x)$ 显然单增，且 $f(1) = 0$（可以验证 $1$ 是函数的拐点），则有
不妨设 $x_1 < x_2$，则 $0 < x_1 < 1 < x_2$ 。待证不等式 $x_1 + x_2 > 2$ 转化为 $x_1 > 2-x_2$ ，不等号两边均落在单增区间上，转化为 $f(x_1) > f(2-x_2)$ ，利用 $f(x_1) + f(x_2) = 0$ 转化为 $-f(x_2) > f(2-x_2)$ ，构造函数
$$ g(x) = f(x) + f(2-x)\quad x > 1 $$求导证明 $g(x) < 0$ 恒成立即可，过程略。
相信看到这里，你已经掌握了拐点偏移的解法（其实东西不多）