先来看一道题目:
问题
已知 $A(-1,0),B(3,0)$,$P$ 是圆 $O:x^2+y^2=45$ 上的一个动点,则 $\sin\angle APB$ 的最大值为 $\underline{\qquad\quad}$ .
设变量爆算是可行的,不过本题的背景是所谓的“最大张角问题”,这类问题有一种巧妙的几何解法。
首先画出本题的图像:
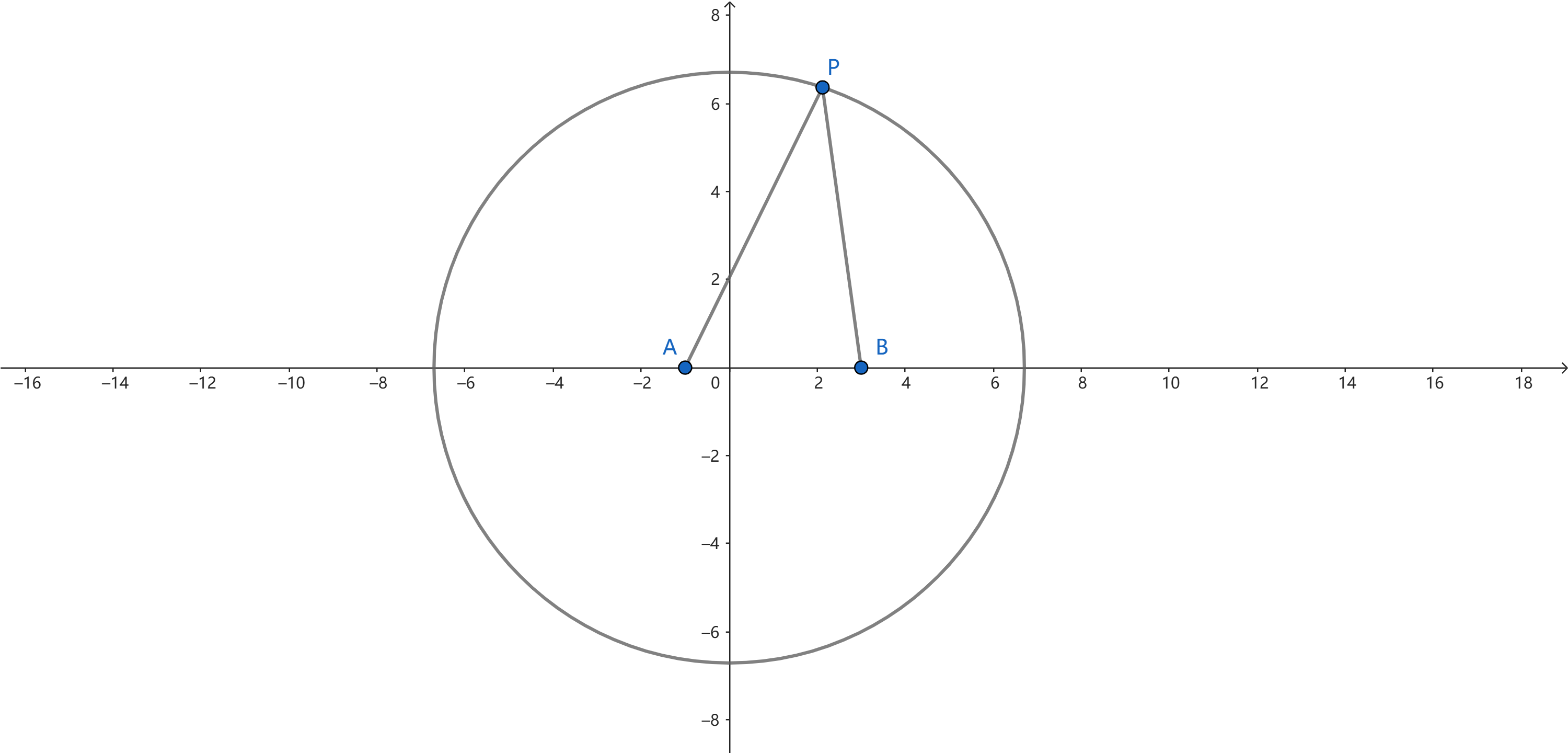
显然 $\angle APB$ 是一个锐角(因为 $P$ 与圆的左右顶点连线所成的角是直角),于是求 $\sin \angle APB$ 的最大值,等价于求张角 $\angle APB$ 的最大值。另外考虑到对称性,不妨设 $P$ 位于圆的上半部分。
现在,我们作一个圆:它经过 $A,B$ 两点,且内切于圆 $O$ ,切点为 $C$ ,如下:
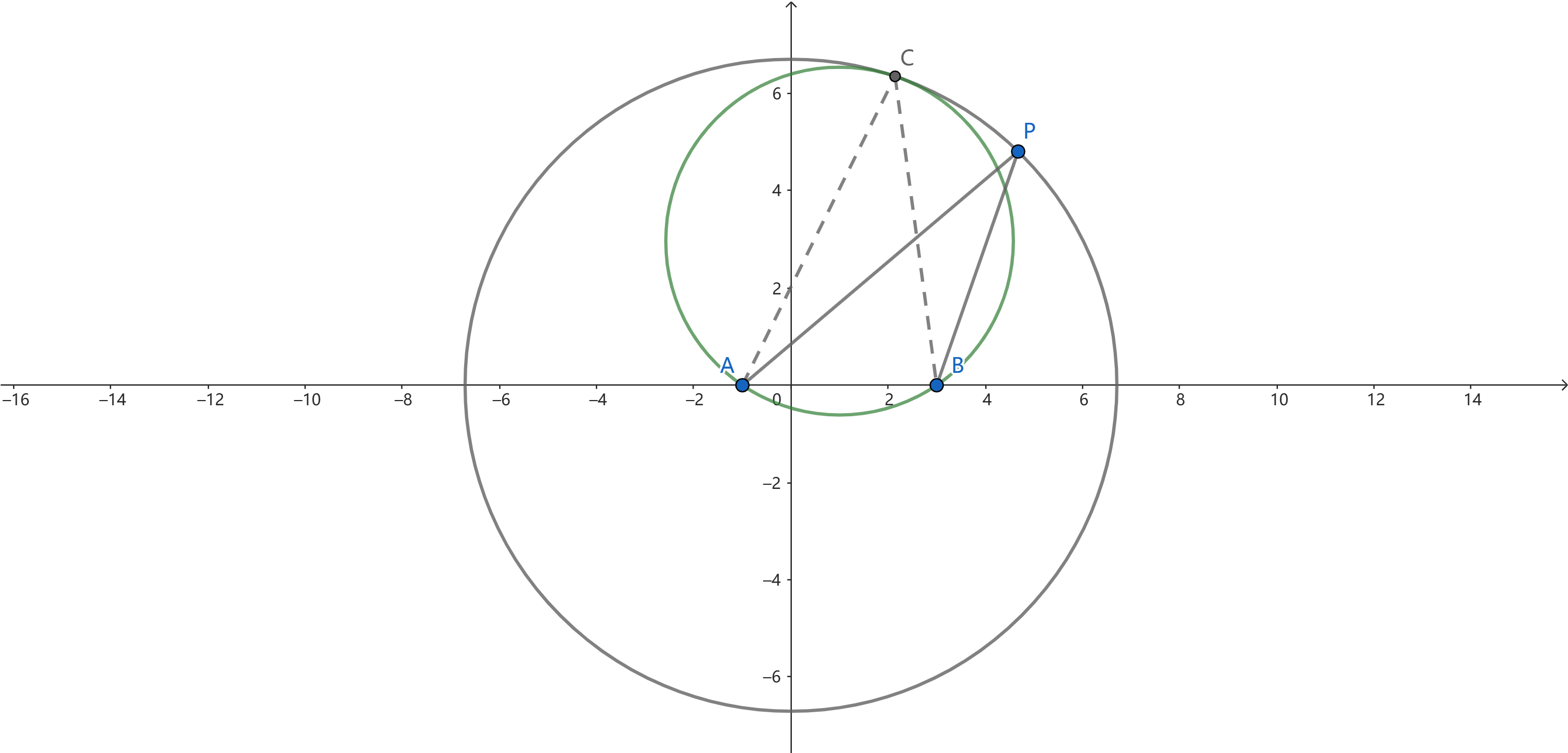
不难发现当 $P$ 与 $C$ 重合时,$\angle APB$ 最大。这基于一个常识:弦所对的圆周角,一定比圆外一点对弦张成的角大,一定比圆内一点对弦张成的角小。
下面只需要求出这个内切于圆 $O$ 的圆即可。设其方程为:$(x-1)^2 + (y-t)^2 = t^2 + 4$,联立方程:
根据 $\Delta = 0$ 可求得 $t = \frac{2\sqrt{55}}{5}$ ,进一步可以求出切点 $C$ 的坐标与 $\sin \angle ACB$ 。
与“最大张角问题”相关的一个定理,称为米勒定理,参见https://zhuanlan.zhihu.com/p/653262335
依据上面的原理,试着解决下面这道题,它来自2020年成都七中高中毕业班三诊模拟
问题
已知 $P$ 是椭圆 $\frac{x^2}{4} + y^2 = 1$ 上一动点,$A(-2,1)$,$B(2,1)$,则 $\cos\angle APB$ 的最大值为 $\underline{\qquad\quad}$ .
答案是 $\frac{\sqrt{6}-\sqrt{2}}{4}$ ,作图如下:
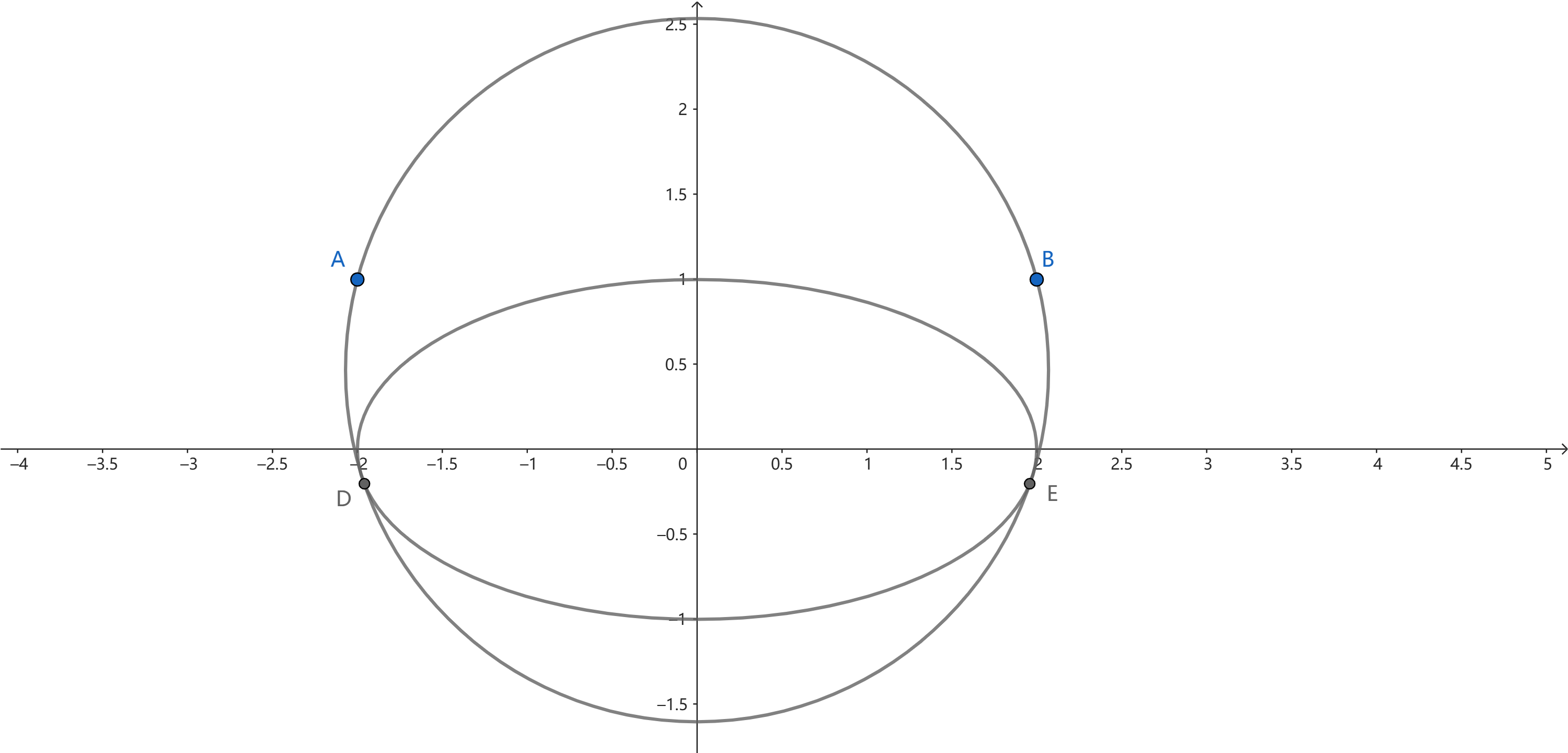
当 $P$ 是切点 $D$ 或 $E$ 时,$\angle APB$ 最小,$\cos \angle APB$ 最大 。