试题
T1
新月
在 $\triangle ABC$ 中,若 $S_{\triangle ABC} = \frac{\sqrt{3}}{4}(a^2+c^2-b^2)$,则 $B=\underline{\qquad\quad}$ .
T2
新月
2022年“极光”最后一卷
在 $\triangle ABC$ 中,角 $A,B,C$ 所对的边分别是 $a,b,c$,且 $a=3$,$b=2$,$\sin A = m$,若 $\triangle ABC$ 唯一确定,则 $m=\underline{\qquad\quad}$ .
T3
上弦月
2022年成都七中高一下期末
在 $\triangle ABC$ 中,若 $AC = 2$,$\frac{1}{\sin B} + \frac{1}{\tan B} = \frac{1}{\sin A} + \frac{1}{\tan A} + 1$ ,则 $\triangle ABC$ 周长的最大值为 $(\qquad\quad)$ .
$A.$ $2\sqrt{5}+4$
$B.$ $2\sqrt{7} + 4$
$C.$ $2\sqrt{5} + 7$
$D.$ $2\sqrt{7} + 7$
T4
上弦月
2024年武汉四调
设 $A,B,C$ 是一个三角形的三个内角,则 $\cos A(3\sin B + 4\sin C)$ 的最小值为 $\underline{\quad\qquad}$ .
T5
上弦月
在 $\triangle ABC$ 中,$\frac{1}{\tan A}, \frac{1}{\tan B}, \frac{1}{\tan C}$ 依次成等差数列。则 $B$ 的最大值为 $\underline{\qquad\quad}$ .
T6
上弦月
在 $\triangle ABC$ 中,$3\sin A + 4\sin B + 18\sin C$ 的最大值为 $\underline{\qquad\quad}$ .
T7
上弦月
2016江苏卷
在锐角三角形 $\triangle ABC$ 中,若 $\sin A = 2\sin B\sin C$,则 $\tan A\tan B\tan C$ 的最小值为 $\underline{\qquad\quad}$ .
T8
上弦月
2022年新高考一卷
已知 $\triangle ABC$ 满足 $\frac{\cos A}{1+\sin A} = \frac{\sin 2B}{1+\cos2B}$ .
(1) 若 $C = \frac{2\pi}{3}$,求 $B$ .
(2) 求 $\frac{a^2+b^2}{c^2}$ 的最小值 .
T9
上弦月
2025年武汉二调
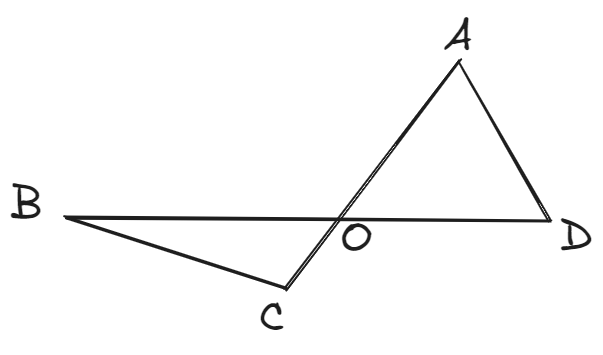
如图,$\triangle AOD$ 与 $\triangle BOC$ 存在对顶角 $\angle AOD = \angle BOC = \frac{\pi}{4}$,$AC=2$,$BD=2\sqrt{2}$,且 $BC = AD$ .
(1) 证明:$O$ 为 $BD$ 中点 .
(2) 若 $\sqrt{5}\sin2A + \cos B = \sqrt{5}$,求 $OC$ 的长 .
答案
T1
答案:$\frac{\pi}{3}$
提示:由 $a^2 + c^2 - b^2$ 联想到余弦定理 $\cos B = \frac{a^2 + c^2 - b^2}{2ac}$ ,再把面积 $S$ 用 $\frac{1}{2}ac\sin B$ 表达。
T2
答案:$1$
提示:显然如果 $A$ 不是直角,那么在锐角域 $(0,\frac{\pi}{2})$ 和钝角域 $(\frac{\pi}{2},\pi)$ 一定能分别找到两个 $A_1,A_2$,满足 $A_1 + A_2 = \pi$ 且 $\sin A_1 = \sin A_2 = m$ 。
T3
答案: $A$
提示:本题的条件式难以化简,不妨从目标式着手,对待求的周长作化简。考虑到条件式是关于角的,因此用正弦定理进行边化角:
到这里我们发现有 $\frac{1}{\sin B} + \frac{1}{\tan B}$。它可以用条件式替换成关于 $A$ 的式子,这样一来就变成单变量的函数了:
$$ \begin{align*} a + b + c&= 2 + 2\sin A\Big(\frac{1}{\sin A} + \frac{1}{\tan A} + 1\Big) + 2\cos A\\ &= 4 +2\sin A + 4\cos A\\ &\leq 4 + 2\sqrt{5} \end{align*} $$上面的解法看似十分自然,其实不容易想到。因为绝大多数的此类问题都是需要化简条件式,最后把化简结果代入目标式,而本题逆其道而行之。参见 b站 上的一个视频: 法一神来之笔!法二恐怖如斯!_哔哩哔哩_bilibili 。
T4
答案: $-\frac{125\sqrt{3}}{108}$
提示:本题比较难。
有三个变量,那么肯定要消元。观察结构,最自然的想法是先消去 $A$ :
到这里有两个变量,肯定要固定主元 。我们把 $B$ 作为主元,$C$ 看作参数,于是
$$ \begin{align*} &(\sin B\sin C-\cos B\cos C)(3\sin B+4\sin C)\\ &=3\sin C\sin^2 B + 4\sin^2 C\sin B - 3\cos C\sin B\cos B - 4\sin C\cos C\cos B\\ &= f(B) \end{align*} $$我们希望能求出上面这个关于 $B$ 的函数 $f(B)$ 的最小值,然而遗憾的是,无论是用三角恒等变换直接对 $f(B)$ 进行化简,还是动用导数,都无法求解其最小值。
此路不通,我们换一种思路,先消去 $B$ :
$$ \begin{align*} \cos A(3\sin B+4\sin C) &= \cos A(3\sin(A+C)+4\sin C)\\ &=\cos A(3\sin A\cos C+3\cos A\sin C +4\sin C)\\ &= (3\cos^2 A+4\cos A)\sin C + 3\sin A\cos A\cos C \end{align*} $$把 $C$ 作为主元,$A$ 看作参数,上面这个关于 $C$ 的函数可以用辅助角公式求出最小值:
$$ \begin{align*} &(3\cos^2 A+4\cos A)\sin C + 3\sin A\cos A\cos C\\ &= \sqrt{(3\cos^2 A+4\cos A)^2 +9\sin^2 A\cos ^2 A}\sin(C+\varphi)\\ &\geq -\sqrt{(3\cos^2 A+4\cos A)^2 +9\sin^2 A\cos ^2 A} \end{align*} $$再求上面这个关于 $A$ 的函数的最小值:
$$ \begin{align*} &-\sqrt{(3\cos^2 A+4\cos A)^2 +9\sin^2 A\cos ^2 A}\\ &= -\sqrt{9\cos^4 A+24\cos^3 A+16\cos^2 A + 9(1-\cos^2 A)\cos ^2A}\\ &= -\sqrt{24\cos^3 A +25\cos ^2 A} \end{align*} $$令 $x = \cos A\in(-1,1)$,考虑函数 $g(x) = 24x^3 +25x^2$ 的最大值。这需要用导数
$$ g'(x) = 72x^2 + 50 x $$所以,$g(x)_{max} = g(-\frac{25}{36})$ 。从而
$$ \cos A(3\sin B +4\sin C)_{min} = -\sqrt{g(-\frac{25}{36})} = -\frac{125\sqrt{3}}{108} $$等号成立当且仅当 $\cos A = -\frac{25}{36}$ 且 $\tan C = \frac{3\sin A}{3\cos A +4} = \cdots$ ,其中第二个条件是根据辅助角公式得到的。
T5
答案:$\frac{\pi}{3}$
提示:由题意有 $\frac{2}{\tan B} = \frac{1}{\tan A} + \frac{1}{\tan C}$ ,显然 $\tan B$ 是正数(否则会出现两个钝角),考虑消元,根据结构特点应该消去 $B$ 。用 $\tan B = -\tan(A+C)$ 代入得
由于 $(\tan A + \tan C)^2\geq 4\tan A\tan C$ ,故 $2\tan A\tan C(\tan A\tan C-1)\geq 4\tan A\tan C$,解得 $\tan A\tan C \leq 0$ 或 $\tan A\tan C \geq 3$ 。于是
$$ \begin{align*} \frac{4}{\tan^2 B} &= \Big(\frac{1}{\tan A} + \frac{1}{\tan C}\Big)^2\\ &=\frac{(\tan A+\tan C)^2}{\tan^2 A\tan ^2 C}\\ &= \frac{2(\tan A\tan C - 1)}{\tan A\tan C}\\ &= 2-\frac{2}{\tan A\tan C}\\ &\geq 2- \frac{2}{3}\\ &= \frac{4}{3} \end{align*} $$故 $\tan B \leq \sqrt{3}$,$B\leq \frac{\pi}{3}$ 。
T6
答案:$\frac{35\sqrt{7}}{4}$
提示:与 T4 一样,考虑消元,这里消去 $A$ :
然后把 $B$ 作为主元,$C$ 视作参数:
$$ \begin{align*} &(3\cos C + 4)\sin B + 3\sin C\cos B + 18\sin C\\ &= \sqrt{(3\cos C+4)^2 + 9\sin^2 C}\sin (B + \varphi) +18\sin C\\ &\leq \sqrt{(3\cos C+4)^2 + 9\sin^2 C} + 18\sin C\\ &=\sqrt{25 + 24\cos C} +18\sin C \end{align*} $$考虑函数 $f(x) = \sqrt{25 + 24\cos x} + 18\sin x (0 < x < \pi)$ 的最大值,用导数求解:
$$ \begin{align*} f'(x) &= -\frac{12\sin x}{\sqrt{25+24\cos x}} +18\cos x\\ \end{align*} $$令 $f'(x) = 0$,
$$ \begin{align*} 2\sin x &= 3\cos x\sqrt{25 +24\cos x}\\ \iff4(1-\cos ^2x) &= 9\cos^2x(25+24\cos x)\\ \iff 4 - 4t^2 &= 225t^2 + 216t^3\\ \iff 216\cos^3 x +229\cos^2x - 4&=0\\ \iff(8\cos x-1)(27\cos ^2x + 32\cos x + 4) &=0 \end{align*} $$(这里最大的困难是看出一个根为 $\frac{1}{8}$) 解得 $\cos x = \frac{1}{8}$ 或 $\cos x = \frac{2\sqrt{37} - 16}{27}$ 或 $\cos x = \frac{-2\sqrt{37} - 16}{27}$ (舍去) 。不难分析出 $\cos x = \frac{1}{8}$ 对应的才是函数 $f(x)$ 的极大值点(也是最大值点),所以
$$ f(x)_{max} = \sqrt{25 + 24\times\frac{1}{8}} + 18\times\frac{\sqrt{63}}{8}=\frac{35\sqrt{7}}{4} $$综合上述过程,取到该最小值当且仅当 $\cos C = \frac{1}{8}$ 且 $\tan B = \frac{3\sin C}{3\cos C + 4} =\frac{9\sqrt{7}}{35}$ ,其中第二个条件是根据辅助角公式得到的。
T7
答案:$8$
提示:$\sin A = 2\sin B\sin C$ 根据结构特点应该先考虑消去 $A$,得
根据三角形中的正切恒等式 :$\tan A +\tan B + \tan C = \tan A\tan B\tan C$,以及 $\tan A + \tan B + \tan C = \tan A + 2\tan B\tan C \geq 2\sqrt{2\tan A\tan B \tan C}$ ,得 $\tan A\tan B\tan C \geq 2\sqrt{2\tan A\tan B \tan C}$ ,从而 $\tan A\tan B\tan C \geq8$ 。等号成立当且仅当 $B = C$ 。
注:三角形中常见的三个恒等式:
$\tan A + \tan B + \tan C = \tan A\tan B\tan C$
$\cos^2 A + \cos^2 B + \cos^2 C +2\cos A\cos B\cos C = 1$
$\frac{1}{\tan\frac{A}{2}\tan\frac{B}{2}} + \frac{1}{\tan\frac{B}{2}\tan\frac{C}{2}} + \frac{1}{\tan\frac{C}{2}\tan\frac{A}{2}} = 1$
T8
答案:(1) $\frac{\pi}{6}$ (2) $4\sqrt{2} - 5$
提示:先处理条件式,只是常规的三角恒等变换
进而得到 $C = \frac{\pi}{2} +B$ ,于是三个角元都可以用 $B$ 表示,这为第二问的消元求取值范围作铺垫。
对于第二问,显然应该边化角:
等号成立当且仅当 $\cos^2 B = \frac{\sqrt{2}}{2}$,根据 $A = \frac{\pi}{2} - 2B$ 知 $B < \frac{\pi}{4}$,所以只能是 $\cos B = \frac{1}{\sqrt[4]{2}}$ 。
T9
答案: (1) 略 (2) $\frac{2}{3}$
提示: 本题的难点在于第一问,要求学生在这样一个显然有平面几何背景的图形中,用高中的解三角形方法从代数上证明几何关系。这很像解析几何的思想。
第一问,需要证明 $BO = OD$,题目的条件中已知对角和对边(尽管 $BC$ 和 $AD$ 的具体数值不明),那么应该用正弦定理:
由于 $BC = AD$,故上下两个连等式应该全相等,对于连等式常常设其等于 $k$ ,于是
$$ \begin{align*} BO &= k\sin C\\ OD &= k\sin A\\ CO &= k\sin B\\ OA &= k\sin D \end{align*} $$我们要证明 $BO = OD$,即证明 $\sin C = \sin A$,要么 $C = A$,要么 $A + C = \pi$,从图上看应该是后一种情况。
由 $BD = BO + OD = 2\sqrt{2}$,$AC = CO + OA = 2$ 得到
接下来要处理这个方程组,这就考验数学素养了,核心思想还是老生常谈的消元。首先,$k$ 可以通过上下之比消去:
$$ \frac{\sin C + \sin A}{\sin B + \sin D} = \sqrt{2} $$我们期望得到 $A,C$ 之间的关系,那么应该把 $B,D$ 消去。根据三角形内角和,$B = \frac{3\pi}{4} - C$,$D = \frac{3\pi}{4} - A$,于是
$$ \begin{align*} \frac{\sin C + \sin A}{\sin(\frac{3\pi}{4}-C) + \sin(\frac{3\pi}{4} - A) } &= \sqrt{2}\\ \iff \frac{\sin C + \sin A}{\frac{\sqrt{2}}{2}(\sin C +\cos C + \sin A + \cos A) } &=\sqrt{2}\\ \iff \sin C + \sin A &= \sin C + \cos C + \sin A + \cos A\\ \iff\cos C + \cos A &= 0\\ \iff A + C &= \pi \end{align*} $$这就证明了 $\sin C = \sin A$,从而 $BO = OC$ 。
以上是本人第一次做这个题目时的方法,下面是官方答案,比较简洁:

第二问,由于在第一问中我们已经得到 $A + C = \pi$,而条件式也可以写成:
$$ \sqrt{5}\sin 2A + \cos(\frac{3\pi}{4} - C) = \sqrt{5} $$于是 $A,C$ 都可以求出来,进而可以求出 $B,D$,那么在 $\triangle OBC$ 中,三个角都知道,$OB = \sqrt{2}$ 也可以从第一问的结论中得到,从而 $OC$ 容易求得。