试题
T1
新月
已知函数 $f(x) = x^3+ax^2+bx+c(a,b,c\in\mathbb{R})$,若不等式 $f(x) > 0$ 的解集为 $\{x|x > m,\text{且}x\neq n\}$ ,且 $n - m = 1$,则函数 $f(x)$ 的极大值为( )
$A.$ $\frac{1}{4}$
$B.$ $\frac{4}{27}$
$C.$ $0$
$D.$ $\frac{4}{9}$
T2
新月
2021年全国乙卷[理]
设 $a\neq0$,若 $x = a$ 为函数 $f(x) = a(x-a)^2(x-b)$ 的极大值点,则 $(\qquad\quad)$ .
$A.$ $a < b$
$B.$ $a > b$
$C.$ $ab < a^2$
$D.$ $ab > a^2$
T3
新月
2025年江苏新高考基地学校第一次大联考
已知三次函数 $f(x) = 2ax(x-b)^2$ 的定义域和值域都是 $[a,b]$,则 $b = \underline{\qquad\quad}$ .
T4
上弦月
2024苏州调研卷
若 $\sin\frac{\pi}{10}$ 是函数 $f(x) = ax^3 - bx + 1(a,b\in\mathbb{N^*})$ 的一个零点,则 $f(1) = \underline{\qquad\quad}$ .
T5
上弦月
2024年广东省广州市高三调研
(多选)设直线 $y = t$ 与 $f(x) = x(x-3)^2$ 的图像的三个交点分别为 $A(a,t),B(b,t),C(c,t)$,且 $a < b < c$,则 $(\qquad)$ .
A. $f(x)$ 图像的对称中心为 $(2,2)$
B. $abc$ 的取值范围是 $(0,12)$
C. $ac$ 的取值范围是 $(0,4)$
D. $c-a$ 的取值范围是 $(3,2\sqrt{3}]$ .
T6
上弦月
2017年江苏卷[理]
已知函数 $f(x) = x^3 +ax^2 + bx + 1(a > 0,b\in\mathbb{R})$ 有极值,且导函数 $f'(x)$ 的极值点是 $f(x)$ 的零点 .
(1) 求 $b$ 关于 $a$ 的函数关系式,并写出定义域 .
(2) 证明:$b^2 > 3a$ .
(3) 若 $f(x)$,$f'(x)$ 这两个函数的所有极值之和不小于 $-\frac{7}{2}$,求 $a$ 的取值范围 .
T7
上弦月
2019 年江苏卷[理]
设函数 $f(x) = (x-a)(x-b)(x-c)$,$a,b,c\in\mathbb{R}$,$f'(x)$ 为 $f(x)$ 的导函数.
(1) 若 $a = b = c$,$f(4) = 8$,求 $a$ 的值.
(2) 若 $a\neq b$,$b = c$,且 $f(x)$ 与 $f'(x)$ 的零点均在集合 $\{-3,1,3\}$ 中,求 $f(x)$ 的极小值.
(3) 若 $a = 0$,$0 < b \leq 1$,$c = 1$,且 $f(x)$ 的极大值为 $M$,求证:$M \leq \frac{4}{27}$ .
T8
满月
设函数 $f(x) = x^3 + ax$($a\in\mathbb{R}$),定义函数 $y = g(x)$ 在 $x = m$ 处的函数值为关于 $x$ 的方程 $f(f(x)) = m$ 的不同实根个数。若 $\{g(x)|x\in\mathbb{R}\} = \{1,5,9\}$,求 $a$ 的值 .
T9
满月
2016 年天津卷
设函数 $f(x) = (x-1)^3 -ax - b$,$x,a,b\in\mathbb{R}$ .
(1) 求 $f(x)$ 的单调区间 .
(2) 若 $f(x)$ 存在极值点 $x_0$,且 $f(x_1) = f(x_0)$,其中 $x_1\neq x_0$,求证:$x_1 + 2x_0 = 3$ .
(3) 设 $a > 0$,函数 $g(x) = |f(x)|$,求证:$g(x)$ 在区间 $[0,2]$ 上的最大值不小于 $\frac{1}{4}$ .
答案
T1
答案:$B$
提示:由题意,函数 $f(x)$ 有两个零点 $m,n$,其中 $n$ 为重根,则
求导 $f'(x) = (x-m-1)(3x-3m-1)$ ,故 $f(x)$ 的极大值为 $f(m+\frac{1}{3}) = \frac{4}{27}$ 。
T2
答案: $D$
提示:若 $a > 0$,则 $a < b$;若 $a < 0$,则 $a > b$,无论哪种情况都有 $ab > a^2$ 。
T3
答案:$5$
提示:$\frac{\pi}{5}$,$\frac{\pi}{10}$ 的三角函数值一般有两种方法求解:构造顶角为 $\frac{\pi}{5}$ 的等腰三角形(黄金三角形);利用三倍角公式。下面我们用三倍角公式进行推导。
根据三倍角公式:$\sin 3x = 3\sin x - 4\sin^3 x$,我们有
到这里可以求出经典的 $\cos\frac{\pi}{5} = \frac{\sqrt{5}+1}{4}$ ,进而根据二倍角公式求出 $\sin\frac{\pi}{10} = \frac{\sqrt{5}-1}{4}$ 。下面计算:
$$ \begin{align*} f(\sin\frac{\pi}{10}) &= a\Big(\frac{\sqrt{5}-1}{4}\Big)^3 - b\Big(\frac{\sqrt{5}-1}{4}\Big) + 1\\ &= \frac{a}{8}(\sqrt{5}-2)-\frac{b}{4}(\sqrt{5}-1)+1\\ &= \Big(-\frac{a}{4}+\frac{b}{4}+1\Big)+\Big(\frac{a}{8}-\frac{b}{4}\Big)\sqrt{5} \end{align*} $$故 $-\frac{a}{4} + \frac{b}{4} + 1 = 0$ 且 $\frac{a}{8} - \frac{b}{4} = 0$,解得 $a = 8$,$b = 4$,从而 $f(1) = 8-4+1 = 5$ 。
顺带一提,$\frac{\pi}{5}$ 这个角的特殊之处是它的二倍角和三倍角之和等于 $\pi$,所以它的三角函数值能够用上面的方法求出根号解。
T4
答案:$\frac{3}{2}$
提示:首先注意到 $f(b) = 0$,则定义域要包含 $0$ ,知 $a < 0, b\geq 0$, 求导 $f'(x) = 2a(x-b)(3x-b)$ ,于是在定义域 $[a,b]$ 上,有
由题意,有 $\frac{8ab^3}{27} = a$ 且 $2a^2(a-b)^2 = b$,解得 $b = \frac{3}{2}$ 。
T5
答案:$ACD$
提示:本题考察了三次函数的两个知识点:
三次函数 $y=ax^3+bx^2+cx+d$ 的对称中心为二阶导数的零点(称为拐点),即 $-\frac{b}{3a}$ ;
三次方程 $ax^3 + bx^2 + cx + d = 0$ 的根 $x_1,x_2,x_2$ 满足韦达定理:
$$ \left\{ \begin{align*} x_1 + x_2 + x_3 &= -\frac{b}{a}\\ x_1x_2 + x_2x_3 +x_3x_1 &= \frac{c}{a}\\ x_1x_2x_3 &= -\frac{d}{a} \end{align*} \right. $$
对于 $BCD$ 选项,由题意知 $a,b,c$ 是三次方程 $x(x-3)^2 = t$ 的三个根,展开得
$$ x^3 - 6x^2 + 9x - t = 0 $$于是由三次方程的韦达定理得 $a+b+c = 6$,$ab+bc+ca=9$,$abc = t$ 。
$B$ 选项:由于 $abc = t$,只需要考虑 $t$ 的范围,画出 $f(x)$ 的图像后易得。
$C$ 选项:$ac = 9-b(a+c) = 9 - b(6-b) = (b-3)^2$,只需要考虑 $b$ 的范围,同样根据 $f(x)$ 的图像易得。
$D$ 选项:$c - a = \sqrt{(c+a)^2 - 4ac} = \sqrt{(6-b)^2 - 4[9-b(a+c)]} = \sqrt{(6-b)^2-4[9-b(6-b)]}$ ,也是只需要考虑 $b$ 的范围。
T6
答案:(1) $(3,+\infty)$ (2) 略 (3) $(3,6]$
提示: 前两问比较简单,题目的意思是说 $f(x)$ 的对称中心恰好为一个零点,根据此条件容易求出 $b = \frac{2a^2}{9} + \frac{3}{a}$,而 $a$ 的范围可根据 $f'(x)$ 有两个零点,即 $\Delta > 0$ 来求解,解得 $a > 3$ 。
第三问,$f'(x) = 3x^2 + 2ax + b$ ,设 $f(x)$ 的极值点为 $x_1,x_2$,则
$f'(x)$ 的极值为 $b - \frac{a^2}{3}$ ;
$f(x)$ 的极值之和为
还有一种更简便的算法: $f(x)$ 的对称中心为 $(-\frac{a}{3}, 0)$ ,而 $f(x_1),f(x_2)$ 关于对称中心对称,故 $f(x_1) + f(x_2) = 0$ 。
综上,$f(x)$ 与 $f'(x)$ 的极值之和为 $b - \frac{a^2}{3} = -\frac{a^2}{9} + \frac{3}{a}$ ,其中 $a >3$,根据 $-\frac{a^2}{9} + \frac{3}{a} \geq -\frac{7}{2}$,解得 $a \leq 6$,故 $3 < a \leq 6$ 。
T7
答案: (1) $2$ (2) $-32$ (3) 略
提示: 前两问比较简单。
第三问,$f(x) = x(x-1)(x-b)$ ,需要求出极大值 $M$,有两种方法:
法一:求导 $f'(x) = 3x^2-2(b+1)x+b$ ,设其两个零点分别为 $x_1,x_2$,且 $x_1 < x_2$,我们想要的是极大值点 $x_1$,当然可以根据求根公式得到
$$ x_1 = \frac{b+1 - \sqrt{b^2-b+1}}{3} $$但是如果把这一大坨奇形怪状的东西直接代入 $f(x_1)$ 进行计算也太抽象了,比较好的方法是:注意到 $0 < x_1 < b \leq 1$ ,我们可以把 $b$ 放缩成 $1$ :
$$ \begin{align*} f(x_1)&\leq x_1(x_1-1)(x_1-1)\\ &=x_1(x_1-1)^2 \end{align*} $$然后再考虑函数 $g(x) = x(x-1)^2, 0 < x < 1$,求导易证 $g(x)\leq \frac{4}{27}$,从而 $M=f(x_1)\leq\frac{4}{27}$ 。
法二:前面与法一相同,只不过在求解函数 $x(x-1)^2$ 的最大值时,可以用三元平均值不等式:
$$ \begin{align*} x(x-1)^2 &= x(1-x)(1-x)\\ &= \frac{1}{2}\cdot2x(1-x)(1-x)\\ &\leq \frac{1}{2}\cdot\Big(\frac{2x+1-x+1-x}{3}\Big)^2\\ &=\frac{4}{27} \end{align*} $$等号成立当且仅当 $2x = 1-x$,即 $x = \frac{1}{3}$ 时。
T8
答案:$-3$
提示:本题非常有意思,也颇有难度。
题干其实不难理解,就是作一条平行于 $x$ 轴的直线 $y = m$ 与函数 $f(f(x))$ 的图像相交,交点个数只可能是 $1,5,9$ 个。这里的 $f(f(x)) = (x^3+ax)^3 + a(x^3+ax)$ ,是一个九次函数,把它展开后求导讨论不太现实。
“数缺形时少直观,形缺数时难入微;数形结合百般好,隔离分家万事休”
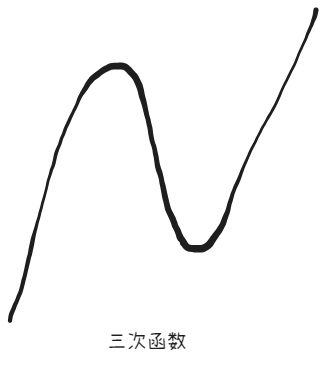
既然从“数”的角度行不通,那么我们来思考这样一个问题:九次函数的图像长什么样子?类比三次函数,三次函数的导数是二次函数,它最多有两个极值点,图像最多“拐”两次:
九次函数的导数是八次函数,所以它最多“拐”八次:
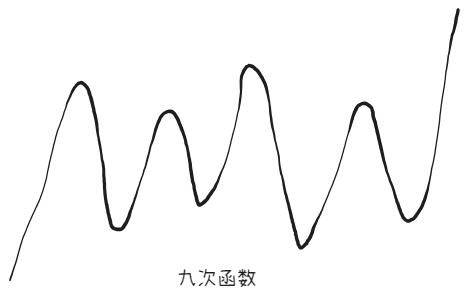
不难发现,只有“拐”八次的情况下,才可能存在 $9$ 个交点:

所以本题的九次函数一定是“拐”八次的,我们记住这个条件。
题目还要求交点个数可以是 $1$ 和 $5$,分别考虑之:
- $1$ 个交点,显然为:
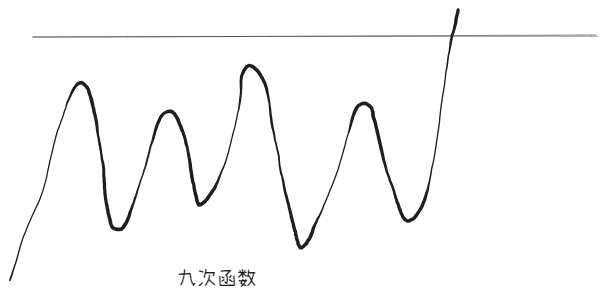
或者:

这是一定可以满足的。
- $5$ 个交点,这种情况比较有意思了。仔细观察上面九次函数的图像,什么时候会和直线有 $5$ 个交点呢?在上面画出的图中,是不可能的,但是如果九次函数长下面这个样子:

其中的所有极大值都相等,所有极小值都相等,那么如果直线经过所有极大值,或者所有极小值,此时的交点个数正好是 $5$ 。
难道除了上面这种极为特殊的情形之外,就不能有 $5$ 个交点了吗?有的兄弟,有的,比如下面这个图:
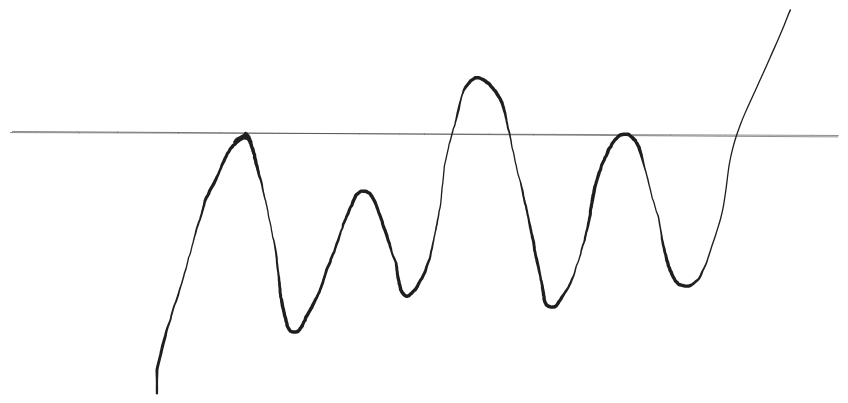
确实也有 $5$ 个交点,但是注意题目要求交点个数只能是 $1,5,9$ 。对于上面这个图,显然交点个数的情形不止这三种,所以是不符合题意的。
综上,我们弄清楚了本题的九次函数需要满足的两条性质:
- 有 $8$ 个极值点;
- 所有极大值都相等,所有极小值都相等。
现在的新问题,就是把这两个性质翻译成数学表达式,从而解出 $a$ 的值。
考虑 $f(f(x))$ 的导数,当然我们不直接对具体的解析式求导,可以使用复合函数求导的链式法则,得到
$$ [f(f(x))]' = f'(f(x))f'(x) $$函数 $f(f(x))$ 的极值点也就是上面函数的零点,即 $f'(f(x))$ 的零点和 $f'(x)$ 的零点。
先考虑 $f'(f(x))$ 的零点,设其中一个为 $x_0$,那么 $f(x_0)$ 应该是 $f'(x)$ 的零点,而 $f'(x)=3x^2+a$,零点为 $\pm\sqrt{-\frac{a}{3}}$(从这里也能看出 $a$ 一定小于 $0$ ),所以 $f(x_0) = \pm\sqrt{-\frac{a}{3}}$ 。下面计算 $f(f(x))$ 的极值 $f(f(x_0))$ :
若 $f(x_0) = \sqrt{-\frac{a}{3}}$,则
$$ \begin{align*} f(f(x_0)) &= f(\sqrt{-\frac{a}{3}})=\frac{2a}{3}\sqrt{-\frac{a}{3}} \end{align*} $$若 $f(x_0) = -\sqrt{-\frac{a}{3}}$,则
$$ f(f(x_0)) = f(-\sqrt{-\frac{a}{3}}) = -\frac{2a}{3}\sqrt{-\frac{a}{3}} $$考虑到正负性,$-\frac{2a}{3}\sqrt{-\frac{a}{3}}$ 应该是函数 $f(f(x))$ 的极大值,$\frac{2a}{3}\sqrt{-\frac{a}{3}}$ 是极小值。
再考虑 $f'(x)$ 的零点,为 $\pm\sqrt{-\frac{a}{3}}$,所以 $f(f(x))$ 的极值为
$$ \begin{align*} f(f(\sqrt{-\frac{a}{3}})) = \frac{2a^2(27-4a^2)}{81}\sqrt{-\frac{a}{3}} \end{align*} $$以及
$$ f(f(-\sqrt{-\frac{a}{3}})) = \frac{2a^2(4a^2-27)}{81}\sqrt{-\frac{a}{3}} $$这两个极值哪个是极大值、哪个是极小值,由 $27-4a^2$ 的正负决定。
如果 $27 - 4a^2 > 0$,即 $-\frac{3\sqrt{3}}{2} < a < 0$,则有
$$ \frac{2a^2(27-4a^2)}{81}\sqrt{-\frac{a}{3}} = -\frac{2a}{3}\sqrt{-\frac{a}{3}} $$解得 $a = 3$ (舍去)。
如果 $27 - 4a^2 < 0$,即 $a < -\frac{3\sqrt{3}}{2}$ ,则有
$$ \frac{2a^2(4a^2-27)}{81}\sqrt{-\frac{a}{3}} = -\frac{2a}{3}\sqrt{-\frac{a}{3}} $$解得 $a = -3$ 或 $\frac{3}{2}$ (舍去)。
所以,$a = -3$ 。
T9
答案:(1) $a \leq 0$ 时,单增区间为 $\mathbb{R}$;$a > 0$ 时,单增区间为 $(-\infty, 1-\sqrt{\frac{a}{3}})$ 和 $(1+\sqrt{\frac{a}{3}},+\infty)$ ;单减区间为 $(1-\sqrt{\frac{a}{3}},1+\sqrt{\frac{a}{3}})$ ; (2) 略 (3) 略
提示:
第一问比较简单。
第二问是三次函数的一个重要性质:对于三次函数 $f(x) = ax^3 + bx^2 + cx + d$ ,设对称中心的横坐标为 $x_0$,一个极值点为 $x_1$,若有 $x_2\neq x_1$ 使得 $f(x_1) = f(x_2)$,则 $2x_1 + x_2 = 3x_0$ 。下面给出证明:
由 $f(x_1) = f(x_2)$ 得
$$ \begin{align*} ax_1^3+bx_1^2+cx_1 &= ax_2^3 + bx_2^2 + cx_2\\ \iff a(x_1^3-x_2^3)+b(x_1^2-x_2^2)+c(x_1-x_2)&= 0\\ \iff a(x_1^2+x_1x_2+x_2^2)+b(x_1+x_2)+c&=0 \qquad\quad(1) \end{align*} $$由 $f'(x_1) = 0$ 得
$$ 3ax_1^2 + 2bx_1 + c = 0\qquad\quad (2) $$两个条件用完了。现在证明 $2x_1 + x_2 = 3x_0 = -\frac{b}{a}$ 。我们设 $t = 2x_1 + x_2$,则 $x_2 = t - 2x_1$,再由 $(2)$ 式得 $x_1^2 = \frac{-c-2bx_1}{3a}$,把这两个式子代入 $(1)$ 式得:
$$ \begin{align*} \frac{-c-2bx_1}{3} + ax_1(t-2x_1)+a(t-2x_1)^2+b(t-x_1)+c &=0\\ \iff at^2 + (b-3ax_1)t + \frac{2c}{3}+2ax_1^2-\frac{5bx_1}{3} &=0\\ \iff at^2 + (b-3ax_1)t+\frac{2c}{3}+\frac{-2c-4bx_1}{3}-\frac{5bx_1}{3} &=0\\ \iff at^2+(b-3ax_1)t-3bx_1 &=0\\ \iff (at+b)(t-3x_1) &= 0 \end{align*} $$解得 $t = -\frac{b}{a}$ 或 $t = 3x_1$,但由于 $x_2 \neq x_1$,故 $t = 2x_1 + x_2 \neq 3x_1$,所以 $t = -\frac{b}{a} = 3x_0$ ,证毕。
第三问,考虑到 $(x-1)^3$ 不太方便,我们设函数 $g(x) = |f(x+1)| = |x^3-ax-a-b|$,再设 $c = -a-b$,则 $g(x) = |x^3 - ax + c|$ 。设在 $[-1,1]$ 上 $g(x)$ 的最大值为 $M$ ,则问题等价于 $M\geq\frac{1}{4}$ 。
这是一个经典问题,背景是 “切比雪夫多项式” 。这个问题有很简洁的解法:
注意到
$$ \begin{align*} g(-1) &= |-1+a+c|\\ g(1) &= |1-a+c|\\ g(\frac{1}{2}) &= |\frac{1}{8}-\frac{a}{2}+c|\\ g(-\frac{1}{2}) &= |-\frac{1}{8} + \frac{a}{2}+c| \end{align*} $$则
$$ \begin{align*} M &\geq \frac{g(-1)+g(1)+2g(-\frac{1}{2})+2g(\frac{1}{2})}{6}\\ &=\frac{|-1+a+c|+|1-a+c|+|\frac{1}{4}-a+2c|+|-\frac{1}{4}+a+2c|}{6}\\ &=\frac{|1-a-c|+|1-a+c|+|-\frac{1}{4}+a-2c|+|-\frac{1}{4}+a+2c|}{6}\\ &\geq \frac{|1-a-c+1-a+c-\frac{1}{4}+a-2c-\frac{1}{4}+a+2c|}{6}\\ &=\frac{1}{4} \end{align*} $$证毕!
一般地,有如下定理:
对任意首一多项式(最高次项系数为 $1$ 的多项式) $f(x) = a_0 + a_1x + a_2x^2 + \cdots + x^n$ ,设 $f(x)$ 在区间 $[-1,1]$ 上的最大值为 $M$,则 $M\geq \frac{1}{2^{n-1}}$ 。等号成立当且仅当 $f(x) \equiv \frac{1}{2^{n-1}}T_n(x)$ ,其中 $T_n(x)$ 为切比雪夫多项式 。
切比雪夫多项式 $T_n(x)$ 的递归定义如下:
- $T_0(x) = 1$
- $T_1(x) = x$
- $T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x)$
可以写出 $T_n(x)$ 的前几项:
$$ \begin{align*} T_1(x) &= x\\ T_2(x) &= 2x^2 - 1\\ T_3(x) &= 4x^3 -3x\\ T_4(x) &= 8x^4 - 8x^2 +1\\ T_5(x) &= 16x^5 - 20x^3 + 5x \end{align*} $$有没有一种似曾相识的感觉?我们熟知:
$$ \begin{align*} \cos x &= \cos x\\ \cos 2x &= 2\cos^2x-1\\ \cos 3x &= 4\cos^3x-3\cos x \end{align*} $$没错,切比雪夫多项式 $T_n(x)$ 就是把 $\cos nx$ 用 $n$ 倍角公式展开后的 $\cos x$ 替换成 $x$ 得到的。
求解本题的时候,我们之所以要取 $g(\pm\frac{1}{2})$ 和 $g(\pm1)$ ,是因为方程 $|T_3(x)| = 1$(或者说 $T_3(x)$ 取到最大值 $1$ 或最小值 $-1$ ) 在区间 $[-1,1]$ 上的所有根为 $\pm \frac{1}{2}, \pm 1$ 。具体解释,参见 最佳逼近 切比雪夫——切比雪夫多项式再研究 - 知乎 (其中还有若干例题可供参考)。
天津卷的这道题,出题人有意把定义域限制在 $[0,2]$ 上,而非 $[-1,1]$ 上(文科卷则没有这样做),还给了一个暗示性很强的函数形式 $(x-1)^3$ ,就是在引导我们先把函数向左平移到 $[-1,1]$ 上。