试题
T1
新月
设函数 $f(x) = \sin x + \frac{1}{2}\sin2x + \frac{1}{3}\sin3x + x$$(0\leq x\leq 2\pi)$ .
(1) 求曲线 $y = f(x)$ 在 $(\pi,f(\pi))$ 处的切线方程 .
(2) 求 $f(x)$ 的单调区间 .
附:$\cos3x = 4\cos^3 x - 3\cos x$
T2
新月
设函数 $f(x) = ax^3 - x^2 - 2\cos x(a\in\mathbb{R})$ .
(1) 若 $a = 0$,求 $f(x)$ 的单调区间.
(2) 若 $f(x)$ 在 $[0,+\infty)$ 上单调递增,求 $a$ 的取值范围.
T3
上弦月
2025年成都七中高三12月阶段性考试
已知 $x(\ln x + 2) \leq ax^2 + \frac{2}{a}\ln x$ 对 $\forall x\geq e$ 恒成立,则实数 $a$ 的取值范围是 $\underline{\qquad\quad}$ .
T4
上弦月
已知函数 $f(x) = a\ln x + x + b - a$ 在区间 $[1,e]$ 上有零点,若 $a^2 + b^2 \geq m$ 恒成立,则 $m$ 的最大值为 $\underline{\qquad\quad}$ .
T5
上弦月
设函数 $f(x) = ax + \sin x + \cos x$,若 $f(x)$ 的图像上存在不同的两点 $A,B$ 使得 $f(x)$ 在 $A,B$ 点处的切线互相垂直,则实数 $a$ 的取值范围是 $\underline{\qquad\quad}$ .
T6
上弦月
2011 年浙江卷
设函数 $f(x) = (x-a)^2\ln x$,$a\in\mathbb{R}$ .
(1) 若 $x = e$ 为 $y = f(x)$ 的极值点,求实数 $a$ .
(2) 求实数 $a$ 的取值范围,使得对任意的 $x\in(0,3e]$,恒有 $f(x) \leq 4e^2$ 成立.
T7
上弦月
(1) 证明:当 $x\in(0,\frac{\pi}{2})$ 时,$\tan x > x$ .
(2) 设方程 $\tan x = x$ 的正根从小到大依次排列,第 $n$ 个为 $x_n$ ($n\in\mathbb{N^*}$) . 证明:
T8
上弦月
2022-2023极光杯跨年线上测试
设函数 $f(x) = 3\sin 2x + 2\sin 3x\cos x + ax$,$a\in\mathbb{R}$.
(1) 若 $f(x)$ 在 $(0,f(0))$ 处的切线的倾斜角为 $\frac{\pi}{4}$,求 $a$ .
(2) 若 $f(x)$ 单调递增,求 $a$ 的取值范围.
(3) 证明:对任意 $n\in\mathbb{N^*}$,$\cos 2x + \cos 4x + \cdots + \cos 2^{2n-2}x + \cos 2^{2n-1}x + n \geq 0$ .
T9
上弦月
已知函数 $f(x) = ae^x - \ln{\frac{x}{a}}(a\neq0)$
(1) 当 $x > 0$,$a > 0$ 时,求 $f(x)$ 的零点个数.
(2) 当 $x < 0$,$a < 0$ 时,求 $f(x)$ 的零点个数.
答案
T1
答案: (1) $y = \pi$ (2) 单增区间是 $(0,\frac{\pi}{3})$,$(\frac{\pi}{2}, \frac{3\pi}{2})$ ,$(\frac{5\pi}{3},2\pi)$;单减区间是 $(\frac{\pi}{3}, \frac{\pi}{2})$,$(\frac{3\pi}{2}, \frac{5\pi}{3})$ .
提示:比较简单 .
T2
答案:(1) 单增区间为 $(-\infty, 0)$,单减区间为 $(0,+\infty)$ (2) $[\frac{2}{3\pi}, +\infty)$
提示:第二问即 $3ax^2 - 2x + 2\sin x \geq 0$ 在 $[0,+\infty)$ 恒成立。优先考虑分离参数,当 $x=0$ 时,不等式成立;当 $x > 0$ 时,有
然后判别有无未定式。显然当 $x = 0$ 时,右边是未定式 $\frac{0}{0}$,这说明分参的做法有风险。但如果我们坚持继续讨论函数 $g(x) = \frac{2(x-\sin x)}{3x^2}$ 的性质,容易得出其最大值为 $g(\pi) = \frac{2}{3\pi}$,并非 $x\to0$ 处的极限值,所以 $a\geq \frac{2}{3\pi}$ 。
从端点效应的角度看,本题是典型的“端点效应失效”问题,类似的还有2020年全国一卷理科数学的导数题。我一直对端点效益这种手段、以及恬不知耻的命题人根据端点效应出的劣质导数题深恶痛绝。对于”恒成立求参数取值范围“这种古老的题型,坚持使用最朴素的两种方法——分离参数和分类讨论。
T3
答案:$[\frac{2}{e},+\infty) \cup \{\frac{2}{e^2}\}$
提示:显然 $a > 0$ 。不等式可以写成 $(ax-2)(\ln x - ax) \leq 0$,有两种情形:
- $\ln x - ax \leq 0$ 恒成立,即 $a\geq\frac{1}{e}$ ,此时必须有 $ax-2 \geq 0$ 恒成立,则 $ae-2\geq0$,得 $a\geq\frac{2}{e}$ ,综合两个范围可得 $a\geq\frac{2}{e}$ 。
- $\ln x - ax$ 有两个零点 $x_1,x_2$,不妨设 $x_2$ 是较大的零点,则 $x_2$ 必须也是 $ax-2$ 的零点(从“穿根引线”的角度来看,相当于重根,此时穿根引线不穿过 $x$ 轴),于是 $x_2 = \frac{2}{a}$,即 $\ln \frac{2}{a} - 2 = 0$,解得 $a = \frac{2}{e^2}$ 。这里还有一个比较隐晦的点,那就是较小的零点 $x_1$ 还要满足 $x_1 \leq e$(因为在 $x_1$ 处,穿根引线会穿过 $x$ 轴),但容易验证当 $a=\frac{2}{e^2}$ 时,确实有 $x_1 < e$ ,因为 $\ln e - \frac{2}{e^2}\cdot e > 0$ 。
T4
答案: $\frac{1}{2}$
提示:套路题。有两种方法:
- 设零点为 $x_0$,则 $a\ln x_0 + x_0 + b - a = 0$,写成 $b = (1-\ln x_0)a - x_0$,可以看成直线的斜截式方程,点 $(a,b)$ 在这条直线上,则 $a^2 + b^2$ 就是点 $(a,b)$ 到原点距离的平方,其最小值就是原点到该直线的距离的平方,即 $(a^2+b^2)_{min} = \frac{x_0^2}{(1-\ln x_0)^2+1}$,求导后容易证明函数 $\frac{x^2}{(1-\ln x)^2+1}$ 是单调递增的,其最小值在 $x_0 = 1$ 处取到,为 $\frac{1}{2}$ 。
- 设零点为 $x_0$,则 $a\ln x_0 + x_0 + b - a = 0$,根据柯西不等式:
可得 $0 = (1 - \ln x_0)a - b - x_0 \leq \sqrt{[(\ln x_0 - 1)^2 + 1](a^2+b^2)} - x_0$ ,于是 $a^2 + b^2 \geq \frac{x_0^2}{(1-\ln x_0)^2+1}$,之后同上。
这类题目的源头是 2022年天津卷导数题:
已知 $f(x) = e^x - a\sin x$,$g(x) = b\sqrt{x}$,若函数 $f(x)$ 与 $g(x)$ 的图像有公共点,证明:$a^2 + b^2 > e$ .
T5
答案:$[-1,1]$
提示:$f'(x) = a + \cos x - \sin x$,由题意知存在 $x_1\neq x_2$,使得
成立,关键是如何翻译这个条件。假设 $f'(x)$ 的值域是 $[b,c]$,其中 $b < 0$,$c > 0$,容易知道 $f'(x_1)f'(x_2)$ 的取值范围是 $[bc, c^2]$ 。所以,只需要保证 $bc \leq -1$ 即可。
容易求出 $f'(x)$ 的值域为 $[a-\sqrt{2}, a+\sqrt{2}]$,所以 $a^2 - 2 \leq -1$ ,解得 $-1 \leq a \leq 1$ 。
T6
答案:(1) $e$ 或 $3e$ (2) $[3e - \frac{2e}{\sqrt{\ln(3e)}}, 3e]$
提示: 本题也是典中典中典,教科书级别的导数题。
第一问根据 $f'(e) = 0$ 求出 $a = e$ 或 $a = 3e$,但是这只是极值点的必要条件,还要检验是否为“变号”零点,经检验两个解都符合题意。
第二问是一个典型的“恒成立求参数取值范围”问题,(按照我的原则)优先考虑分离参数。首先显然当 $x < 1$ 时,不等式肯定成立;于是考虑 $x > 1$,就有:
进而
$$ x - \frac{2e}{\sqrt{\ln x}} \leq a \leq x + \frac{2e}{\sqrt{\ln x}} $$你可能会想:这么奇怪的函数能求最值?还真能。实际上,只要没有出现未定式,我们都可以放心地求导、求最值。首先左边的函数显然单增,于是
$$ a \geq 3e - \frac{2e}{\sqrt{\ln 3e}} $$右边的函数求导后可知其最大值在 $x = e$ 的时候取到,为 $3e$,则
$$ a \leq 3e $$综上,$3e - \frac{2e}{\sqrt{\ln 3e}} \leq a \leq 3e$ 。
这道题目之所以称为经典,除了考场上不太敢用的分参(因为 $a$ 在平方内),还在于解法的多样性。其实本题也可以正常对 $f(x)$ 求导讨论,用隐零点的方法解决,读者不妨一试。
T7
答案:略
提示:
第一问是平凡的,意义在于提示了第二问需要使用不等式 $\tan x > x$ 。
第二问,显然 $n\pi < x_n < (n+\frac{1}{2})\pi$ ,由于 $x_n$ 和 $x_{n+1}$ 不在 $\tan x$ 的同一个单调区间上,自然要想到把它们都转化到同一单调区间 $(0, \frac{\pi}{2})$ 上。由于 $x_n - n\pi \in (0, \frac{\pi}{2})$ ,这就完成了转化,其中的 $n\pi$ 是可以通过 $\tan x$ 的周期性消去的。于是
由于 $x_{n+1} > x_n$,故 $\tan (x_{n+1} - (n+1)\pi) > \tan (x_n - n\pi)$ ,利用 $(0,\frac{\pi}{2})$ 上的单调性得
$$ x_{n+1} - (n+1)\pi > x_n - n\pi $$即 $x_{n+1} - x_n > \pi$ ,左边不等式得证。
直觉上,右边的不等式不能像左边一样简单通过单调性证明,肯定需要放缩,而题目第一问明确提示了不等式 $\tan x > x$ ,这个不等式的成立条件是 $0 < x < \frac{\pi}{2}$,注意到 $x_{n+1} - x_n - \pi \in (0, \frac{\pi}{2})$,故
整理得 $x_{n+1} - x_n - \pi < \frac{\pi}{x_nx_{n+1}}$,又因为 $x_n > n\pi$,$x_{n+1} > (n+1)\pi$,故
$$ x_{n+1} - x_n - \pi < \frac{\pi}{n(n+1)\pi^2} = \frac{1}{(n^2+n)\pi} $$右边不等式得证。
贯穿本题始终的一个思想,就是把 $x_n$ 和 $x_{n+1}$ 分别减去 $n\pi$ 和 $(n+1)\pi$,转化到同一单增区间 $(0,\frac{\pi}{2})$ 上。这样不仅能利用 $\tan x$ 的单调性解决左边不等式,还能用不等式 $\tan x > x$ 解决右边不等式。
T8
答案: (1) $-11$ (2) $[6,+\infty)$ (3) 略
提示:本题的第一个难点是三角恒等变换:
其中用到了积化和差:
$$ \begin{align*} \cos \theta \cos \alpha &= \frac{1}{2}\Big[\cos(\theta+\alpha) + \cos(\theta - \alpha)\Big]\\ \sin\theta\sin\alpha &=\frac{1}{2}\Big[\cos(\theta-\alpha)-\cos(\theta+\alpha)\Big] \end{align*} $$第二问,由 $f'(x)\geq 0$ 知 $a-6\geq0$,则 $a\geq6$ 。
第三问,首先需要思考前两问提示了我们什么不等式。在求解第二问的过程中,我们计算出了
从而
$$ \begin{align*} 2\cos 2x + \cos4x &\geq -\frac{3}{2}\\ 2\cos4x + \cos 8x &\geq -\frac{3}{2}\\ 2\cos8x + \cos 16x &\geq -\frac{3}{2}\\ \cdots\\ 2\cos2^{2n-2}x + \cos2^{2n-1}x&\geq -\frac{3}{2} \end{align*} $$把这 $2n-2$ 个不等式累加,得到
$$ 2\cos 2x + 3(\cos 4x + \cos 8x + \cdots+\cos2^{2n-2}x) + \cos 2^{2n-1}x\geq3-3n $$又因为 $\cos 2x + 2\cos 2^{2n-1}x \geq -3$ (显然),把上面的式子加上这部分,就有
$$ \begin{align*} \cos 2x + \cos 4x + \cdots + \cos2^{2n-1}x \geq -n \end{align*} $$证毕。
本题与 2020年全国二卷[理] 的导数题非常相似:
已知函数 $f(x) = \sin^2x\sin2x$ .
(1) 讨论 $f(x)$ 在区间 $(0,\pi)$ 的单调性.
(2) 证明:$|f(x)|\leq \frac{3\sqrt{3}}{8}$ .
(3) 设 $n\in\mathbb{N^*}$,证明:$\sin^2x\sin^22x\sin^24x\cdots\sin^22^nx \leq \frac{3^n}{4^n}$ .
T9
答案:(1) $0 < a < \frac{1}{e}$ 时两个零点;$a = \frac{1}{e}$ 时一个零点;$a > \frac{1}{e}$ 时无零点。 (2) $-e \leq a < 0$ 时一个零点;$a > -e$ 时三个零点。
提示:本题精彩至极。
先求导: $f'(x) = ae^x - \frac{1}{x} = \frac{axe^x - 1}{x}$ 。
第一问有 $a > 0, x > 0$,则 $axe^x - 1$ 是递增的,而且显然有一个零点 $x_0$,就是 $f(x)$ 的最小值点。考虑到当 $x\to 0$,$f(x)\to -\infty$;当 $x\to+\infty$,$f(x)\to +\infty$,故 $f(x)$ 的零点个数完全由最小值 $f(x_0)$ 的正负性决定。这是一个隐零点问题,隐零点 $x_0$ 满足 $ax_0e^{x_0} - 1 = 0$,下面计算的时候,优先考虑把参数 $a$ 消去:
$$ \begin{align*} f(x_0) &= ae^{x_0} - \ln\frac{x_0}{a}\\ & = \frac{1}{x_0} - x_0 - 2\ln x_0 \end{align*} $$构造函数 $g(x) = \frac{1}{x} - x - 2\ln x$,求导容易证明 $g(x)$ 单减,再考虑到 $g(1) = 0$,故我们有:
- 当 $0 < x_0 < 1$,即 $f'(1) > 0 \Longrightarrow a > \frac{1}{e}$ 时,$f(x_0) > 0$,$f(x)$ 无零点;
- 当 $x_0 = 1$,即 $f'(1) = 0 \Longrightarrow a = \frac{1}{e}$ 时,$f(x_0) = 0$,$f(x)$ 有一个零点;
- 当 $x_0 > 1$,即 $f'(1) < 0 \Longrightarrow 0 < a < \frac{1}{e}$ 时,$f(x_0) < 0$,$f(x)$ 有两个零点。
第二问,重新审视一下 $axe^x - 1$ 这个函数,求导易证其先增后减,最大值在 $x = -1$ 处,为 $-\frac{a}{e} - 1$,再考虑到 $x\to0$ 时,$axe^x - 1\to -1$;$x\to -\infty$ 时,$axe^x - 1 \to - 1$ 。于是这个函数的零点(对应着 $f(x)$ 的极值点)根据其最大值 $-\frac{a}{e}-1$ 的正负,有三种情形:
- 当 $-\frac{a}{e}-1 < 0$ ,即 $a > -e$ 时,$f'(x) > 0$ 恒成立(注意分母的 $x$ 是负的),$f(x)$ 单调递增。再由 $x\to 0$ 时,$f(x)\to+\infty$;$x\to -\infty$ 时,$f(x)\to -\infty$,故此时 $f(x)$ 有一个零点;
- 当 $-\frac{a}{e}-1 = 0$,即 $a = -e$ 时,$f'(x)\geq0$ 恒成立,跟上面一样,$f(x)$ 有一个零点;
- 当 $-\frac{a}{e} - 1 < 0$,即 $a < -e$ 时,$axe^x - 1$ 有两个零点 $x_1,x_2$,图象大致如下:
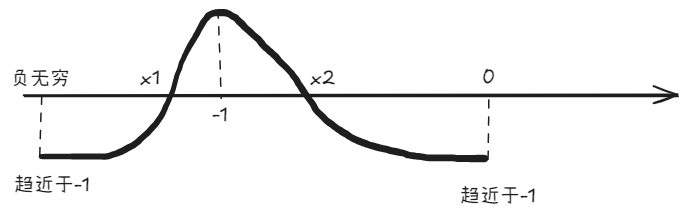
这里的 $x_1, x_2$ 应该分别是 $f(x)$ 的极大值点和极小值点(还是因为 $f'(x)$ 分母的 $x$ 是负的)。于是函数 $f(x)$ 的图像大致如下:
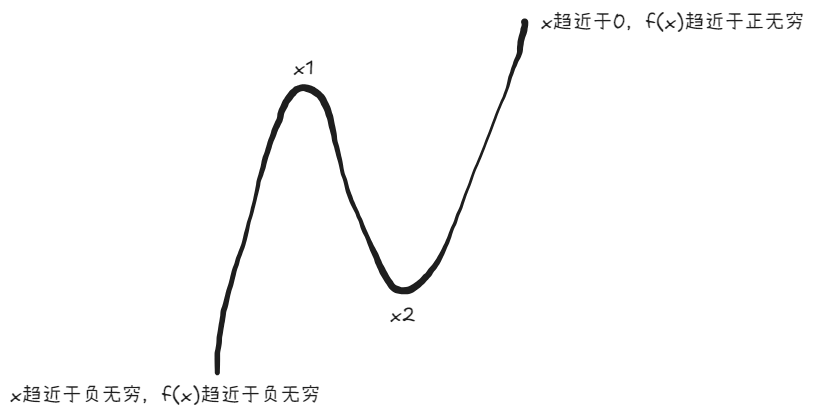
于是 $f(x)$ 的零点个数由极大值 $f(x_1)$ 和极小值 $f(x_2)$ 的正负决定。这又是一个隐零点问题,隐零点 $x_1,x_2$ 满足方程 $axe^x - 1 = 0$,跟第一问类似,计算出:
$$ \begin{align*} f(x_1) &= \frac{1}{x_1} - x_1 - 2\ln (-x_1)\\ f(x_2) &= \frac{1}{x_2} - x_2 - 2\ln (-x_2) \end{align*} $$注意由于 $x_1,x_2$ 是负的,$\ln x_1^2$ 应该等于 $2\ln (-x_1)$,这里跟第一问是不一样的。
要判断 $f(x_1),f(x_2)$ 的正负性,我们构造函数 $h(x) = \frac{1}{x} - x - 2\ln(-x), x < 0$,求导容易证明 $h(x)$ 是单调递减的,再考虑到 $h(-1) = 0$,以及 $x_1 < -1 < x_2$ ,可得 $f(x_1) > 0$,$f(x_2) < 0$,从而函数 $f(x)$ 有三个零点。
第二问很有趣,$f(x)$ 的零点个数随着 $a$ 的改变,直接跳过了“两个零点”的情形,只可能是一个零点或者三个零点。