试题
T1
新月
2025年湖北省”圆创联盟“第三次联合测评
(多选)已知函数 $f(x) = \cos^2\frac{\omega x}{2} + \frac{\sqrt{3}}{2}\sin\omega x - \frac{1}{2}(\omega > 0)$,则 $(\qquad\quad)$ .
$A. f(x) = \sin\big(\omega x +\frac{\pi}{6}\big)$
$B.$ $f(x)$ 在区间 $(0,\frac{\pi}{6\omega})$ 上单调递增
$C.$ 若 $f(x)$ 在区间 $(0,\pi)$ 上恰有一个极值点,则 $\omega$ 的取值范围是 $(\frac{1}{3},\frac{4}{3})$
$D.$ 若 $f(x)$ 在区间 $(\pi,2\pi)$ 内没有零点,则 $\omega$ 的取值范围是 $(0,\frac{5}{12}] \cup [\frac{5}{6},\frac{11}{12})$
T2
新月
2024星云二月调研
已知函数 $f(x) = \sin2x + a\cos 2x$ ,将 $f(x)$ 的图像向左平移 $\frac{\pi}{6}$ 个单位长度,所得图像与曲线 $y = f(x)$ 关于原点对称,则 $a = (\qquad\quad)$ .
$A.$ $\frac{\sqrt{3}}{3}$
$B.$ $-\frac{\sqrt{3}}{3}$
$C.$ $\sqrt{3}$
$D.$ $-\sqrt{3}$
T3
上弦月
2024年武汉二调
如图,在函数 $f(x) = \sin(\omega x + \varphi)$ 的部分图像中,若 $\overrightarrow{TA} = \overrightarrow{AB}$ ,则点 $A$ 的纵坐标为 $(\qquad\quad)$ .
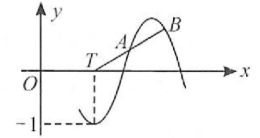
$A.$ $\frac{2-\sqrt{2}}{2}$
$B.$ $\frac{\sqrt{3}-1}{2}$
$C.$ $\sqrt{3}-\sqrt{2}$
$D.$ $2 - \sqrt{3}$
T4
上弦月
2025年广州一模
已知 $\omega > 0$,曲线 $y = \cos\omega x$ 与 $y = \cos(\omega x - \frac{\pi}{3})$ 相邻的三个交点构成一个直角三角形,则 $\omega = \underline{\qquad\quad}$ .
T5
上弦月
2024年加速杯
设 $\alpha \in (0,\frac{\pi}{2})$,$\beta \in (\frac{\pi}{2},\pi)$,且 $\tan\alpha = \sin(\alpha+\beta)$,则 $(\qquad\quad)$ .
$A.$ $\tan\alpha + \tan(\alpha+\beta) < 0$
$B. \cos\alpha + \cos(\alpha+\beta) < 0$
$C.$ $\sin\frac{\beta}{2} + \sin(\alpha - \frac{\pi}{2}) > 0$
$D.$ $\sin\frac{\beta}{2} + \cos(\alpha + \beta) > 0$
T6
上弦月
2025年江苏新高考基地学校第一次大联考
记函数 $f(x) = \sin 2x$,$x\in[0,\frac{\pi}{2}]$ 的图像为曲线 $C$,直线 $y=m$ 与 $C$ 交于 $A,B$ 两点,直线 $y = 6m$ 与 $C$ 交于 $D,E$ 两点,若 $|AB| = 2|DE|$,则 $m=$ $\underline{\qquad\quad}$ .
T7
上弦月
2019-2020衡水中学高三第二学期质检四
若函数 $f(x) = lg[\sin(\pi x)\cdot\sin(2\pi x)\cdot\sin(3\pi x)\cdot\sin(4\pi x)]$ 的定义域与区间 $[0,1]$ 的交集由 $n$ 个开区间组成,则 $n$ 的值为 $(\qquad)$ .
$A$. $2$
$B.$ $3$
$C.$ $4$
$D.$ $5$
T8
上弦月
已知函数 $f(x) = 6\cos (\omega x + \varphi)$,其中 $\omega > 0$ 且 $0 < \varphi < \pi$ . 对 $\forall x \in \mathbb{R}$ 都有 $f(x)\leq|f(\frac{\pi}{6})|$,且 $x = -\frac{\pi}{6}$ 是 $f(x)$ 的一个零点. 若曲线 $y = f(x) - 6$ 在 $(\frac{\pi}{15},\frac{\pi}{6})$ 上有且仅有一个零点,则 $\omega$ 的最大值为 $\underline{\qquad\quad}$ .
T9
上弦月
2024年星云五月调研
$1593$ 年,韦达发表了圆周率无穷乘积公式,这是第一个可以直接用于计算圆周率到任意精度的古典公式. 推导过程如下:因为
且当 $n\to+\infty$ 时,$2^n\sin\frac{\alpha}{2^n}\to\alpha$,所以 $\cos\frac{\alpha}{2}\cos\frac{\alpha}{4}\cdots\cos\frac{\alpha}{2^{n-1}}\cos\frac{\alpha}{2^n}\cdots = \frac{\sin\alpha}{\alpha}$ .
根据以上信息,$\frac{\sqrt{2 + \sqrt{2}}}{2}\times\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\times\frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}\times\cdots = (\qquad\quad)$ .
$A.$ $\frac{1}{\pi}$
$B.$ $\frac{\sqrt{2}}{\pi}$
$C.$ $\frac{2}{\pi}$
$D.$ $\frac{2\sqrt{2}}{\pi}$